ПРОЧНОСТНОЙ РАСЧЕТ КОНСТРУКЦИИ | Энциклопедия Кругосвет
Содержание статьиПРОЧНОСТНОЙ РАСЧЕТ КОНСТРУКЦИИ, начальный этап проектирования конструкции, на котором определяются действующие на нее силы.
Соотношение между расчетом и проектированием.
Главная задача здесь – подобрать наиболее подходящие материалы и размеры для элементов конструкции так, чтобы последние надежно выдерживали те нагрузки, которые будут действовать на них во время работы конструкции. Здание или мост собирается из таких основных элементов конструкции, как балки и сжатые или растянутые стержни. Чтобы можно было рассчитать элементы, из которых будет состоять мост, инженер должен сначала определить нагрузки и оценить различные связанные с ними эффекты. Например, чтобы рассчитать стальную балку, нужно сначала определить нагрузки и реакции, действующие силы и моменты и точки их приложения. Если проектируется ферма (состоящая из сжатых и растянутых стержней), то нужно определить нагружение каждого стержня. На этом этапе проектирования, называемом предварительным прочностным расчетом, балка и ферма существуют лишь в виде линейных (одномерных) диаграмм.
На следующем этапе определяются пропорции и выбираются размеры. При этом, однако, проектировщик не анализирует распределение напряжений и деформаций внутри элементов конструкции. Максимально допустимые напряжения для каждого материала, например среднеуглеродистой стали, предписываются соответствующими нормативами. Руководствуясь ими, проектировщик рассчитывает элементы конструкции так, чтобы эти максимально допустимые напряжения не были превышены в наиболее нагруженных сечениях.
Основные факторы прочностного расчета.
Равновесие сил.
Важнейшую роль в прочностном расчете конструкции играет закон равновесия сил. Инженер-прочнист занимается в основном проектированием конструкций, выдерживающих действие различных эксплуатационных нагрузок. Хотя силы и моменты могут создаваться не только статическими нагрузками, сама конструкция должна оставаться устойчивой. Следовательно, для элемента конструкции, лежащего в определенной плоскости и нагруженного в этой плоскости, силы должны уравновешиваться. Это выражается представленными ниже уравнениями для системы несходящихся (не пересекающихся в одной точке) сил, лежащих в одной плоскости:

Эти уравнения означают, что должны быть уравновешены: 1) сумма горизонтальных составляющих сил, 2) сумма вертикальных составляющих сил и 3) сумма моментов сил относительно любой точки в данной плоскости. Если конструкция статически определима, то уравнений (1)–(3) достаточно для анализа эффектов, связанных с данной системой сил.
Если же число неизвестных сил или факторов больше трех, то такая система является статически неопределимой. Она может быть статически неопределимой относительно внешних нагрузок и реакций, как, например, неразрезная балка с двумя пролетами, или внутренне статически неопределимой, как, скажем, ферма с избыточными диагональными стержнями.
Статические и динамические нагрузки.
Нагрузки, действующие на элементы конструкции, делятся на статические (или постоянные) и динамические (или временные). Статические нагрузки действуют в данном положении постоянно. Их часто называют гравитационными, поскольку они направлены по вертикали. К статическим нагрузкам относится вес настила моста, здания, механического оборудования, закрепленного на определенном месте. Динамические же нагрузки могут возникать, исчезать и изменять место своего приложения. Динамические нагрузки создают люди в зданиях, грузовые автомобили на мосту, станки в цеху, гидротурбина в машинном зале ГЭС. Такие более или менее упорядоченные динамические нагрузки нетрудно определить, но есть и другие динамические нагрузки, которые невозможно достоверно оценить заранее, например, обусловленные ветром, ударами, температурными колебаниями и землетрясениями. В этих случаях используются специальные методы прочностного расчета и коэффициенты запаса.
Динамические нагрузки
Это нагрузки, изменяющиеся не только во времени, но и в пространстве.
Для динамических нагрузок характерна относительно большая скорость приложения, что требует при расчетах учитывать инерционную массу как объекта, создающего нагрузку, так и элемента, подвергающегося воздействию нагрузки. Другими словами, следует учитывать характер движения объекта создающего нагрузку, а также то, что инерционные массы элементов конструкции, подвергающиеся воздействию динамической нагрузки, перемещаются с ускорением и влияют на напряженно-деформированное состояние элементов. Чтобы учесть это влияние, в уравнения статического равновесия к внешним и внутренним силам добавляются силы инерции на основании принципа Даламбера. Добавление инерционных сил позволяет рассматривать любую движущуюся систему как находящуюся в состоянии статического равновесия в любой момент времени. Таким образом динамические нагрузки вызывают в материале исследуемого элемента конструкции динамические напряжения и поведение материала при этом оказывается отличным от поведения при статических напряжениях.
В свою очередь динамические нагрузки в зависимости от характера движения бывают также нескольких видов. Для строительных конструкций наиболее важными являются подвижные и ударные нагрузки:
Подвижные нагрузки
Это нагрузки возникающие в результате перемещения некоего объекта по поверхности исследуемой конструкции (вдоль рассматриваемой оси элемента).
Например, автомобиль, проезжающий по мосту, создает подвижную нагрузку на элементы моста. При этом подвижная нагрузка будет зависеть не только от массы автомобиля, но и от его скорости и траектории движения. Например, при движении по окружности центробежная сила будет тем больше, чем больше скорость движения, потому улететь в кювет на плохой дороге на большой скорости — пара пустяков.
Ударные нагрузки
Это нагрузки, возникающие в момент соприкосновения перемещающегося объекта с поверхностью исследуемой конструкции (вдоль или поперек рассматриваемой оси элемента).
Однако и это еще не все варианты классификации нагрузок. По площади приложения нагрузки делятся на сосредоточенные и распределенные.
Сосредоточенные нагрузки
Это силы, площадь приложения которых пренебрежимо мала по сравнению с площадью рассчитываемой конструкции.
Можно сказать, что сосредоточенная нагрузка — это и есть сила, действующая на конструкцию. При этом площадь действия силы не учитывается, а потому измеряется сосредоточенная нагрузка в килограммах или Ньютонах.
Распределенные нагрузки
Это все остальные нагрузки, т.е. силы, распределяющиеся по длине и ширине элемента.
Разнообразие распределенных нагрузок поистине не поддается описанию. Распределенные нагрузки могут равномерно и неравномерно распределенными, равномерно и неравномерно изменяющимися по длине или ширине, при этом характер изменения нагрузки может описываться уравнением параболы, синусоиды, окружности, овала и любым другим уравнением.
А самое примечательное во всем этом то, что один и тот же человек в зависимости от ситуации может рассматриваться и как сосредоточенная нагрузка и как распределенная, и как статическая и как динамическая и только постоянной нагрузкой человек быть не может.
В целом все это выглядит не совсем понятно, однако ничего страшного в этом нет, как говорится, лучше один раз рассчитать конструкцию, чем 100 раз прочитать, как это делается. Примеров расчета на сайте хватает. А кроме того, понимание основ сопромата позволяет в большинстве случаев определять нагрузки так, чтобы максимально упростить расчет.
Физические величины
Чтобы правильно и без ошибок задать физическую величину, нужно знать ее величину измерения и числовое значение. Физическая величина состоит из произведения численного значения величины на ее единицу измерения. Численное значение показывает, во сколько раз физическая величина больше ее единицы.
Очень большие или наоборот, очень малые числовые значения становятся более понятны и лучше читаемы, когда обозначаются при помощи приставок перед названием единицы. Единицы физических величин, которые соответствуют основным единицам международной системы обозначения единиц СИ, очень облегчают восприятие и документирование физических процессов.
ДИНАМИЧЕСКАЯ НАГРУЗКА — это… Что такое ДИНАМИЧЕСКАЯ НАГРУЗКА?
- ДИНАМИЧЕСКАЯ НАГРУЗКА
меняющаяся нагрузка, возникающая в движущихся частях механизмов и машин при движении подвижного состава по верхнему строению пути, при ударах и т. п.
Технический железнодорожный словарь. — М.: Государственное транспортное железнодорожное издательство. Н. Н. Васильев, О. Н. Исаакян, Н. О. Рогинский, Я. Б. Смолянский, В. А. Сокович, Т. С. Хачатуров. 1941.
.
- ДИНАМИТЫ
- ДИНАМОМАШИНА
Смотреть что такое «ДИНАМИЧЕСКАЯ НАГРУЗКА» в других словарях:
Динамическая нагрузка — Динамическая нагрузка – нагрузка, изменение величины, направления или положения которой происходит настолько быстро, что при расчете сооружения необходимо учитывать инерционные силы. [Отраслевой руководящий документ. Техническая… … Энциклопедия терминов, определений и пояснений строительных материалов
ДИНАМИЧЕСКАЯ НАГРУЗКА — (строительная механика) нагрузка, для которой характерно быстрое изменение во времени ее значения и направления (напр., под действием ветра) … Большой Энциклопедический словарь
ДИНАМИЧЕСКАЯ НАГРУЗКА — (Dynamic pressure) нагрузка на разные сооружения и механизмы, нарастающая до полной своей величины в весьма короткие промежутки времени порядка периода собственных колебаний данного сооружения или механизма. Самойлов К. И. Морской словарь. М. Л … Морской словарь
динамическая нагрузка — — [Е.С.Алексеев, А.А.Мячев. Англо русский толковый словарь по системотехнике ЭВМ. Москва 1993] Тематики информационные технологии в целом EN DLdynamic loadtransient load … Справочник технического переводчика
динамическая нагрузка — 29 динамическая нагрузка FA Нагрузка, вызванная ускорениями при движении и остановке рабочей платформы с расположенным на ней испытательным грузом, масса которого предусмотрена в нормативных и конструкторских документах для проведения… … Словарь-справочник терминов нормативно-технической документации
динамическая нагрузка — нагрузка, характеризующаяся быстрым изменением во времени её значения, направления или точки приложения и вызывающая в элементах конструкции значительные силы инерции. * * * ДИНАМИЧЕСКАЯ НАГРУЗКА ДИНАМИЧЕСКАЯ НАГРУЗКА (строительная механика),… … Энциклопедический словарь
динамическая нагрузка — dinaminė apkrova statusas T sritis automatika atitikmenys: angl. dynamic load; dynamical load vok. dynamische Belastung, f rus. динамическая нагрузка, f pranc. charge dynamique, f … Automatikos terminų žodynas
динамическая нагрузка — dinaminė apkrova statusas T sritis fizika atitikmenys: angl. dynamic load; dynamical load vok. dynamische Belastung, f rus. динамическая нагрузка, f pranc. charge dynamique, f … Fizikos terminų žodynas
Динамическая нагрузка — нагрузка, характеризующаяся быстрым изменением во времени её значения, направления или точки приложения и вызывающая в элементах конструкции значительные силы инерции (См. Сила инерции) … Большая советская энциклопедия
ДИНАМИЧЕСКАЯ НАГРУЗКА — нагрузка, характеризующаяся быстрым изменением во времени её значения, направления или точки приложения. Д. н. может вызывать в элементах конструкции значит. напряжения … Большой энциклопедический политехнический словарь
Динамические нагрузки — Строительная механика
Колебания являются наиболее распространенной формой движения в природе. Инженерные конструкции могут совершать колебанияя от ветра, землетрясения, работы различных машин и механизмов. Опасность колебаний для сооружений заключается в том, что величины и знаки внутренних усилий при этом постоянно изменяются.
Динамика исследует механические колебания конструкций, рассматриваемых как колебательные системы.
Колебательные системы:
– Диссипативная система – это система, у которой происходит диссипация (рассеивание) энергии.
– Консервативная система – это система, для которой рассеиванием энергии пренебрегают.
Примером консервативной колебательной системы может выступать пружина с закрепленной на ее конце массой (рис. 1). Жесткость пружины r характеризует упругость системы, а масса m – ее инерционные свойства.

Рисунок 1. Консервативная система
Примером диссипативной системы может выступать система, состоящая из пружины, вязкого элемента и массы (рис. 2). Сила сопротивления c, возникающая в вязком элементе, стремится прекратить колебания системы. Вязкий элемент называют демпфером (или амортизатором). Поэтому диссипативную систему по другому называют демпфированной системой.

Рисунок 2. Диссипативная система
Причиной возникновения колебаний сооружения являются динамические нагрузки, которые в отличие от статических изменяются во времени по величине, направлению или положению. Они сообщают массам тел системы ускорения, вызывая тем самым инерционные силы, которые приводят к увеличению колебаний, что в результате может привести к разрушению коснтрукции.
Виды динамических нагрузок:
1) Периодическая нагрузка – это нагрузка, которая воздействует на сооружение через определенный период (причиной выступают различные механизмы: электродвигатели, металлообрабатывающие станки, вентиляторы и др.).
Если их вращающиеся части не уравновешены, то они вызывают гармоническую нагрузку.
Такие механизмы как поршневые компрессоры и насосы, штамповочные машины, дробилки приводят к возникновению негармонической нагрузки.
2) Импульсные нагрузки (взрыв, падающий груз или частяи силовых установок (молотов, копров и др.).
3) Подвижные нагрузки (поезда, автомобили и др.).
4) Недетерминированные (случайные) нагрузки (ветер, сейсмические и взрывные нагрузки).
При динамическом нагружении деформации сооружения зависят не только от уровня внешних воздействий, но и от уровня возникающих сил инерции, которые противоположны по направлению ускорению а массы m.
Закон распределения сил инерции зависит от расположения масс в расчетной схеме. В динамике принято два вида расчетных схем:
1) расчетные схемы с дискретным расположением сосредоточенных (точечных) масс, движение которых характеризуется конечным числом степеней свободы и описываются обыкновенными дифференциальными уравнениями;
2) расчетные схемы с распределенными массами, движение которых характеризуется функциями времени и пространственных координат (бесконечное число степеней свободы) и описываются дифференциальными уравнениями в частных производных.
Для анализа колебаний деформируемых систем в основном применяются расчетные схемы с дискретным расположением масс. В таких расчетных схемах все элементы сооружения считаются невесомыми, а их массу заменяют сосредоточенными массами, расположенными в узловых точках. В этом случае выражение для сил инерции получается наиболее простым.
Для одной сосредоточенной массы сила инерции определяется по формуле:

где Z – перемещение массы.
Для нескольких масс:

где J – вектор обобщенных сил инерции;
М – матрица сосредоточенных масс;
 – вектор ускорений масс.
– вектор ускорений масс.
Кроме динамических нагрузок и сил инерции на характер колебаний деформируемой системы существенное влияние оказывают силы сопротивления движению. В динамике дискретных систем полагается, что силы сопротивления движению Ф(t) пропорциональны и противоположны скоростям перемещений узлов:

где H – матрица коэффициентов сопротивления.
Т.о., в процессе динамической деформации на узлы колеблющейся дискретной системы действуют суммарные внешние динамические силы PD, равные сумме заданных динамических нагрузок P(t), вызванных ими сил инерции J(t), и сил сопротивления движению Ф(t):

динамическая нагрузка — это… Что такое динамическая нагрузка?
- динамическая нагрузка
29 динамическая нагрузка FA
Нагрузка, вызванная ускорениями при движении и остановке рабочей платформы с расположенным на ней испытательным грузом, масса которого предусмотрена в нормативных и конструкторских документах для проведения динамических испытаний
—
8.7. Динамическая нагрузка
Нагрузка, возникающая при перемещении люльки с грузом и элементов подъемника
8.7. Динамическая нагрузка
Нагрузка, возникающая при перемещении люльки с грузом и элементов подъемника
3.1.4 динамическая нагрузка: Нагрузка, характеризующаяся быстрым изменением величины, направления или точки приложения, вызывающим в элементах конструкции силы инерции.
3.1.4 динамическая нагрузка: Нагрузка, характеризующаяся быстрым изменением величины, направления или точки приложения, вызывающим в элементах конструкции силы инерции.
1.9. Динамическая нагрузка — нагрузка, воздействующая на конструкцию или оборудование буровой установки в результате процессов ускорения или замедления движения поднимаемых (опускаемых) грузов.
___________
* В настоящее время действуют Правила безопасности в нефтяной и газовой промышленности ( title=»Правила безопасности в нефтяной и газовой промышленности»), утвержденные постановлением Госгортехнадзора России от 05.06.03 № 56, зарегистрированным Минюстом России 20.06.03 г., регистрационный № 4812 (Примеч. изд.).
3.3 динамическая нагрузка (dynamic load): Нагрузка, характеризующаяся быстрым изменением во времени её значения, направления или точки приложения и вызывающая в элементах конструкции силы инерции.
Смотри также родственные термины:
3.1.7 динамическая нагрузка (грузоподъемность) подшипника: Расчетная максимальная (допускаемая) нагрузка на подшипник при воздействии основной нагрузки.
3.1.7 динамическая нагрузка (грузоподъемность) подшипника: Расчетная максимальная (допускаемая) нагрузка на подшипник при воздействии основной нагрузки.
Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.
- динамическая модель электронного датчика
- динамическая нагрузка (грузоподъемность) подшипника
Смотреть что такое «динамическая нагрузка» в других словарях:
Динамическая нагрузка — Динамическая нагрузка – нагрузка, изменение величины, направления или положения которой происходит настолько быстро, что при расчете сооружения необходимо учитывать инерционные силы. [Отраслевой руководящий документ. Техническая… … Энциклопедия терминов, определений и пояснений строительных материалов
ДИНАМИЧЕСКАЯ НАГРУЗКА — (строительная механика) нагрузка, для которой характерно быстрое изменение во времени ее значения и направления (напр., под действием ветра) … Большой Энциклопедический словарь
ДИНАМИЧЕСКАЯ НАГРУЗКА — (Dynamic pressure) нагрузка на разные сооружения и механизмы, нарастающая до полной своей величины в весьма короткие промежутки времени порядка периода собственных колебаний данного сооружения или механизма. Самойлов К. И. Морской словарь. М. Л … Морской словарь
ДИНАМИЧЕСКАЯ НАГРУЗКА — меняющаяся нагрузка, возникающая в движущихся частях механизмов и машин при движении подвижного состава по верхнему строению пути, при ударах и т. п. Технический железнодорожный словарь. М.: Государственное транспортное железнодорожное… … Технический железнодорожный словарь
динамическая нагрузка — — [Е.С.Алексеев, А.А.Мячев. Англо русский толковый словарь по системотехнике ЭВМ. Москва 1993] Тематики информационные технологии в целом EN DLdynamic loadtransient load … Справочник технического переводчика
динамическая нагрузка — нагрузка, характеризующаяся быстрым изменением во времени её значения, направления или точки приложения и вызывающая в элементах конструкции значительные силы инерции. * * * ДИНАМИЧЕСКАЯ НАГРУЗКА ДИНАМИЧЕСКАЯ НАГРУЗКА (строительная механика),… … Энциклопедический словарь
динамическая нагрузка — dinaminė apkrova statusas T sritis automatika atitikmenys: angl. dynamic load; dynamical load vok. dynamische Belastung, f rus. динамическая нагрузка, f pranc. charge dynamique, f … Automatikos terminų žodynas
динамическая нагрузка — dinaminė apkrova statusas T sritis fizika atitikmenys: angl. dynamic load; dynamical load vok. dynamische Belastung, f rus. динамическая нагрузка, f pranc. charge dynamique, f … Fizikos terminų žodynas
Динамическая нагрузка — нагрузка, характеризующаяся быстрым изменением во времени её значения, направления или точки приложения и вызывающая в элементах конструкции значительные силы инерции (См. Сила инерции) … Большая советская энциклопедия
ДИНАМИЧЕСКАЯ НАГРУЗКА — нагрузка, характеризующаяся быстрым изменением во времени её значения, направления или точки приложения. Д. н. может вызывать в элементах конструкции значит. напряжения … Большой энциклопедический политехнический словарь
Динамическое действие нагрузок
Основные теоретические сведения
Нагрузка, сравнительно быстро меняющая свою величину или положение, называется динамической.
Общий метод расчета, учитывающий динамическую нагрузку, основан на принципе Даламбера, согласно которому движущееся тело можно рассматривать находящимся в состоянии мгновенного равновесия, если к действующим на него внешним силам добавить силу инерции.
При вращательном движении с постоянной угловой скоростью ω сила инерции определяется по формуле:
 (4.1)
(4.1)
где m – масса движущегося тела;
 – центростремительное ускорение;
– центростремительное ускорение;
R – радиус вращения.
Сила инерции всегда направлена в сторону, противоположную ускорению.
Угловая скорость выражается через число оборотов:
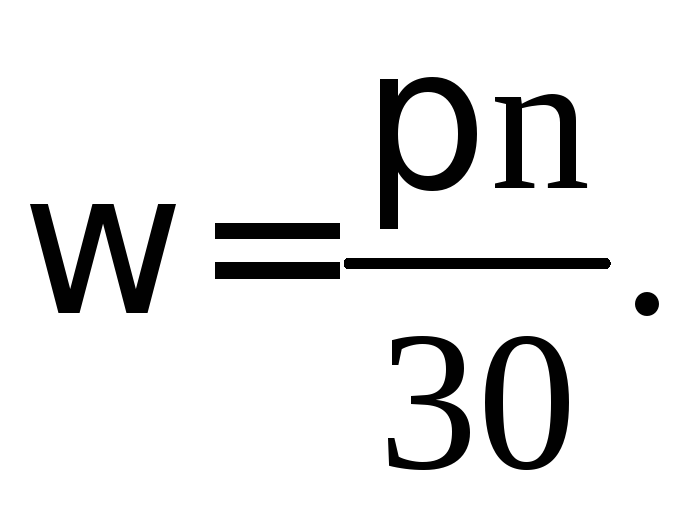 (4.2)
(4.2)
Если силы инерции известны, то для расчета конструкции применяют обычный метод сечений, а для определения внутренних усилий используют уравнение равновесия.
При действии ударной нагрузки (нагрузки чрезвычайно малой продолжительности) определение сил инерции затруднительно. Примером ударного нагружения является удар падающего груза при забивке свай и т. п.
При ударном воздействии груза Р на конструкцию напряжения в ней могут значительно превосходить напряжения в той же конструкции при стати-ческом приложении нагрузки Р. Напряжения, возникающие при ударном нагружении, называют динамическими и определяют их по формуле:
 ,
(4.3)
,
(4.3)
где  – статические напряжения;
– статические напряжения;
 – коэффициент динамики.
– коэффициент динамики.
Коэффициент динамики вычисляют в
зависимости от высоты падения груза h
и статического прогиба  в точке падения груза:
в точке падения груза:
 (4.4)
(4.4)
Статические напряжения и прогиб в точке удара определяют согласно формулам теории изгиба прямых стержней [2, разд. 4].
Решение типовой задачи при ударных воздействиях на конструкцию
На двутавровую балку (двутавр № 20а,  ,
, ),
свободно лежащую на двух опорах (рис.
4.1,а), с высоты h, равной 11 см, падает
груз Р весом 300 Н.
),
свободно лежащую на двух опорах (рис.
4.1,а), с высоты h, равной 11 см, падает
груз Р весом 300 Н.
Найти наибольшие нормальные напряжения
в балке. Решить аналогичную задачу при
условии, что правая опора заменена
пружиной, податливость  (осадка от груза весом 10 кН) которой
равна
(осадка от груза весом 10 кН) которой
равна
1) Для определения наибольшего нормального напряжения в балке сначала приложим вес падающего груза в виде сосредоточенной силы Р в точку падения балки (рис. 4.1, б), с помощью уравнений статики определим реакции опор RАи RВи построим эпюру изгибающих моментов Mz[2, подразд. 4.2, 4.3].
По значению наибольшего изгибающего момента вычислим статические напряжения:
 (4.5)
(4.5)
После подстановки значений Wи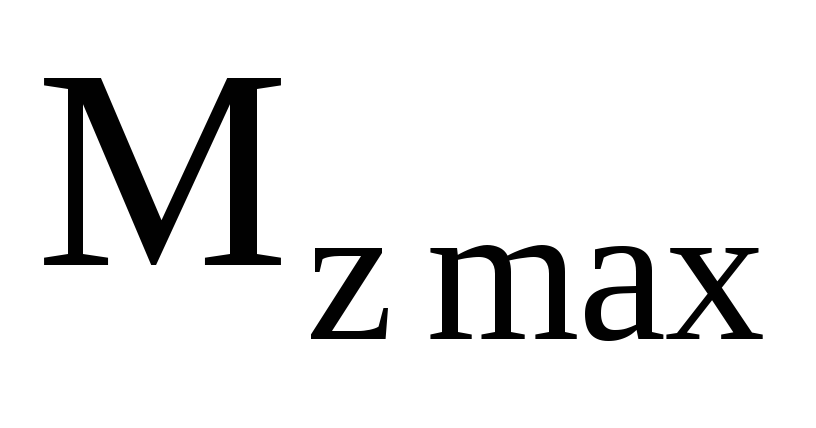 (рис. 4.1,в) в формулу (4.5)
получим:
(рис. 4.1,в) в формулу (4.5)
получим: (МН/м2).
(МН/м2).
Найдем статическое вертикальное
перемещение  (прогиб)
точки удара. Для этого выбираем
вспомогательное единичное состояние,
приложив в точку удара единичную
нагрузку. Вспомогательная эпюра
изгибающих моментов
(прогиб)
точки удара. Для этого выбираем
вспомогательное единичное состояние,
приложив в точку удара единичную
нагрузку. Вспомогательная эпюра
изгибающих моментов (рис. 4.1,д) будет иметь тот же вид,
что и эпюра
(рис. 4.1,д) будет иметь тот же вид,
что и эпюра ,
следует лишь все ординаты эпюры
,
следует лишь все ординаты эпюры уменьшить в 300 раз. Перемножим эпюры
уменьшить в 300 раз. Перемножим эпюры и
и по
формуле Симпсона (4.3) [2]:
по
формуле Симпсона (4.3) [2]:
 (4.6)
(4.6)
где  –
ординаты изгибающих моментов по концам
и посредине каждого участка эпюры Mzi;
–
ординаты изгибающих моментов по концам
и посредине каждого участка эпюры Mzi;
 – соответствующие ординаты эпюры
– соответствующие ординаты эпюры ;
;
 –
модуль упругости стали первого рода
(модуль Юнга).
–
модуль упругости стали первого рода
(модуль Юнга).
Подставляя в формулу (4.6) соответствующие
значения L,Jи для
участков балки AB и BC, получим:
для
участков балки AB и BC, получим:

Вычислим коэффициент динамики (4.4): 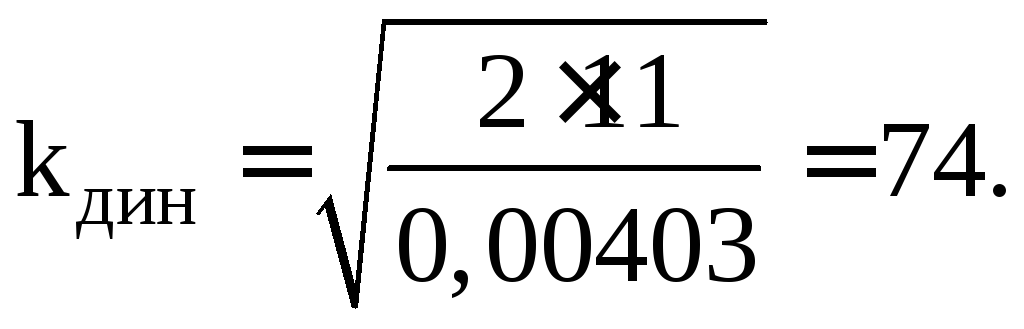
Наибольшие нормальные напряжения в
балке рассчитаем согласно выражению
(4.3):  (МН/м2).
(МН/м2).
2) Заменим правую опору балки пружиной
(рис. 4.1, е). Установленная пружина
увеличивает статическую деформацию в
точке удара. В месте установки пружины
действует сила равная 375 Н (0,375 кН), вызывающая осадку
точки В, которая рассчитывается по
формуле:
равная 375 Н (0,375 кН), вызывающая осадку
точки В, которая рассчитывается по
формуле:
 (4.7)
(4.7)
Из подобия двух треугольников (см. рис. 4.1, е)
 . (4.8)
. (4.8)
После подстановки исходных данных в формулы (4.7), (4.8) получим:



C
Рис. 4.1. Схематическое представление ударного воздействия нагрузки на балку:
а,б,г,е– расчетные схемы; в,д– эпюры изгибающих моментов
Полное перемещение точки удара
определяется как сумма прогиба балки
из первого решения и значения  :
:
В этом случае новый коэффициент динамики вычисляется по формуле:
 (4.9)
(4.9)
наибольшие нормальные напряжения –
 (4.10)
(4.10)
После подстановки исходных данных в
формулы (4.9), (4.10) получим: 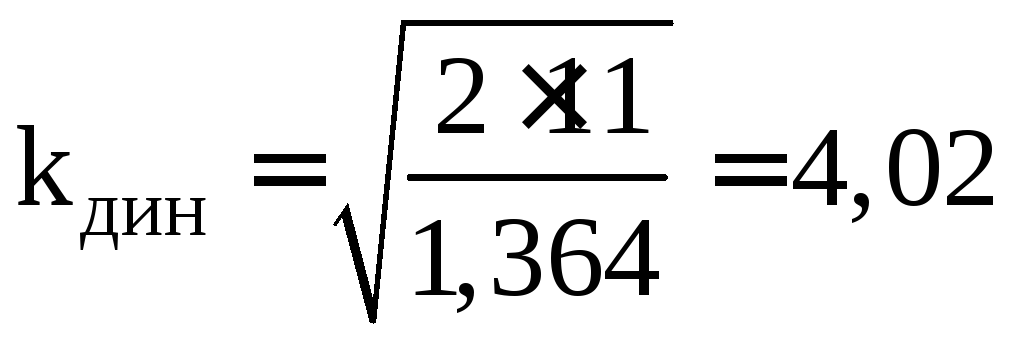 ;
; (МН/м2).
(МН/м2).
Сравнение значений напряжений, полученных в двух вариантах решения задачи, показывает, что при замене правой опоры пружиной нормальные напряжения уменьшатся в 18,4 раза (68,1 : 3,7).
27.Классификация нагрузок (Силовых факторов).
Внешние силы в сопромате делятся на активные и реактивные (реакции связей).Нагрузки – это активные внешние силы.
Нагрузки по способу приложения
По способу приложения нагрузки бывают объемными (собственный вес, силы инерции), действующими на каждый бесконечно малый элемент объема, и поверхностными. Поверхностные нагрузки делятся на сосредоточенные нагрузки ираспределенные нагрузки.
Распределенные нагрузки характеризуются давлением — отношением силы, действующей на элемент поверхности по нормали к ней, к площади данного элемента и выражаются в Международной системе единиц (СИ) в паскалях, мегапаскалях (1 ПА = 1 Н/м2; 1 МПа = 106 Па) и т.д., а в технической системе – в килограммах силы на квадратный миллиметр и т.д. (кгс/мм2, кгс/см2).
В сопромате часто рассматриваются поверхностные нагрузки, распределенные по длине элемента конструкции. Такие нагрузки характеризуются интенсивностью, обозначаемой обычно q и выражаемой в ньютонах на метр (Н/м, кН/м) или в килограммах силы на метр (кгс/м, кгс/см) и т.д.
Нагрузки по характеру изменения во времени
По характеру изменения во времени выделяют статические нагрузки — нарастающие медленно от нуля до своего конечного значения и в дальнейшем не изменяющиеся; идинамические нагрузки вызывающие большие силы инерции.
28.Динамическое, циклическое нагружение, понятие предела выносливости.
Динамическая нагрузка – нагрузка, которая со- провождается ускорением частиц рассматри- ваемого тела или соприкасающихся с ним де- талей. Динамическое нагружение возникает при приложении быстро возрастающих усилий или в случае ускоренно- го движения исследуемого тела. Во всех этих случаях необходимо учитывать силы инерции и возникающее движение масс системы. Кроме того, динамические нагрузки можно подразделить на ударные и повторно-перемен- ные.
Ударная нагрузка (удар) – нагружение, при ко- тором ускорения частиц тела резко изменяют свою величину за очень малый промежуток времени (внезапное приложение нагрузки). Заметим, что, хотя удар и относится к динамическим видам нагружения, в ряде случаев при расчете на удар силами инерции пренебрегают.
Повторно-переменное (циклическое) нагруже- ние – нагрузки, меняющиеся во времени по ве- личине (а возможно и по знаку).
Циклическое нагружение-изменение механических и физических свойств материала под длительным действием циклически изменяющихся во времени напряжений и деформаций.
Преде́л выно́сливости (также преде́луста́лости) — в науках о прочности: одна из прочностных характеристик материала, характеризующих его выносливость, то есть способность воспринимать нагрузки, вызывающие циклические напряжения в материале.
29.Понятие усталости материалов, факторы, влияющие на устойчивость к усталостному разрушению.
Усталость материала — в материаловедении — процесс постепенного накопления повреждений под действием переменных (часто циклических) напряжений, приводящий к изменению его свойств, образованию трещин, их развитию и разрушению материала за указанное время.
Влияние концентрации напряжений
В
местах резкого изменения поперечных
размеров детали, отверстий, проточек,
пазов, резьбы и т.д., как показано в п.
2.7.1, возникает местное повышение
напряжений, значительно снижающее
предел выносливости по сравнению с
таковым для гладких цилиндрических
образцов. Это снижение учитывается
введением в расчеты эффективного
коэффициента концентрации напряжений  ,
представляющего отношение предела
выносливости
,
представляющего отношение предела
выносливости  гладкого
образца при симметричном цикле к пределу
выносливости
гладкого
образца при симметричном цикле к пределу
выносливости образца
тех же размеров, но имеющего тот или
иной концентратор напряжения:
образца
тех же размеров, но имеющего тот или
иной концентратор напряжения:
 .
.
2.8.3.2. Влияние размеров детали
Экспериментально установлено, что с увеличением размеров испытуемого образца предел его выносливости понижается (масштабный эффект). Это объясняется тем, что с увеличением размеров возрастает вероятность неоднородности структуры материалов и его внутренних дефектов (раковины, газовые включения), а также тем, что при изготовлении образцов малого размера имеет место упрочнение (наклеп) поверхностного слоя на относительно большую глубину, чем у образцов больших размеров.
Влияние
размеров деталей на значение предела
выносливости учитывается
коэффициентом  (масштабный
фактор),
представляющим собой отношение предела
выносливости детали заданных размеров
(масштабный
фактор),
представляющим собой отношение предела
выносливости детали заданных размеров  к
пределу выносливости
к
пределу выносливости лабораторного
образца подобной конфигурации, имеющего
малые размеры:
лабораторного
образца подобной конфигурации, имеющего
малые размеры:
 .
.
2.8.3.3. Влияние состояния поверхности
Следы режущего инструмента, острые риски, царапины являются очагом возникновения усталостных микротрещин, что приводит к снижению предела выносливости материала.
Влияние
состояния поверхности на предел
выносливости при симметричном цикле
характеризуется коэффициентом  качества
поверхности,
который представляет собой отношение
предела выносливости
качества
поверхности,
который представляет собой отношение
предела выносливости 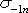 детали
с данной обработкой поверхности к
пределу выносливости
детали
с данной обработкой поверхности к
пределу выносливости тщательно
полированного образца:
тщательно
полированного образца:
 .
.
2.8.3.4. Влияние поверхностного упрочнения
Различные
способы поверхностного упрочнения
(механическое упрочнение, химикотермическая
и термическая обработка) могут существенно
повысить значение коэффициента качества
поверхности (до 1,5 … 2,0 и более раз вместо
0,6 … 0,8 раз для деталей без упрочнения).
Это учитывается при расчетах введением
коэффициента  .
.
2.8.3.5. Влияние асимметрии цикла
Причиной
усталостного разрушения детали являются
длительно действующие переменные
напряжения. Но, как показали эксперименты,
с увеличением прочностных свойств
материала увеличивается их чувствительность
к асимметрии цикла, т.е. постоянная
составляющая  цикла
«вносит свой вклад» в снижение усталостной
прочности. Этот фактор учитывается
коэффициентом
цикла
«вносит свой вклад» в снижение усталостной
прочности. Этот фактор учитывается
коэффициентом .
.
