Пропорция 1 к 3: Пропорция 1 к 3 – это сколько?

Содержание

Как развести бензин для бензопилы: официальный сайт Echotool.

Почему нужно смешивать масло и бензин

Для нормальной работы любому двигателю внутреннего сгорания нужны, как минимум, две вещи:

Топливо — вернее топливовоздушная смесь, приготовленная карбюратором, попадает в камеру сгорания, воспламеняется, расширяется, и «толкает» поршень вниз, за счёт чего выполняется полезная работа.
Смазка — необходима для уменьшения силы трения между соприкасающимися деталями двигателя.

В первую очередь, масло нужно для того, чтобы исключить так называемое «сухое» трение металла о металл. Из-за него контактирующие детали подвергаются критическому износу — появляются задиры, царапины, уменьшается компрессия, снижается ресурс. Также масло нужно для уплотнения зазоров.

Почему же нужно смешивать масло с топливом для бензопилы?

Это требование напрямую связано с особенностями устройства и принципом работы двухтактных двигателей, которыми оснащается данный инструмент.

Смазка деталей кривошипно-шатунного механизма и цилиндропоршневой группы здесь выполняется исключительно за счёт масла, находящегося в горючем. Благодаря особому устройству двигателя, топливовоздушная смесь попадает не только в камеру сгорания, но и в картер, где находится коленвал с шатуном. Таким образом, смазываются все трущиеся детали.

Соотношение количества масла и бензина для топливной смеси

Чтобы двухтактный двигатель бензопилы работал в оптимальном для него режиме, масло с бензином необходимо смешивать в определённых пропорциях. Они обычно указываются в инструкции к инструменту, а также на упаковках со смазкой. Рассмотрим вкратце, что будет, если рекомендуемых соотношений не соблюдать, или нарушать их по ошибке (незнанию).

Если масла добавить в бензин слишком мало, его концентрации не хватит для эффективной смазки трущихся деталей. Двигатель будет издавать звенящие звуки, чрезмерно греться, и быстро выйдет из строя. Много масла — тоже плохо, так как излишки не смогут полноценно сгорать. Это приведёт к образованию нагара на стенках цилиндра и поршне, загрязнению свечи зажигания, выхлопной системы. Также упадёт мощность, повысится расход топлива, и во время работы будет наблюдаться чрезмерная дымность выхлопа.

Чтобы этих проблем избежать, масло с бензином надо смешивать в рекомендуемых производителем пропорциях. Указываются они в виде соотношений — 1:50, 1:40, 1:25 и так далее. Любая из этих пропорций говорит о том, сколько масла нужно лить на объём топлива. Например, для приготовления смеси по пропорции 1:25 понадобится 1 литр масла на 25 литров бензина.

Важно не перепутать! Довольно часто указанные пропорции воспринимаются пользователями наоборот. К примеру, 1:50 понимается, как на 1 литр бензина 50 миллилитров масла. Это грубая ошибка, которая приведёт к повышенной концентрации масла в горючем. На самом деле при таком соотношении на 1 литр масла нужно всего 20 миллилитров масла.

Как не запутаться в пропорциях? Ведь мало кому надо готовить 50, или даже 25 литров топливной смеси для бензопилы. Тем более, что хранить смешанный с маслом бензин долго нельзя. Обычно готовят столько, сколько потребуется на день-два. А с учётом небольшого расхода бензопилы это 1-5 литров.

Есть три способа, как правильно развести бензин для бензопилы в небольших объёмах:

Поделить 1000 на вторую цифру в пропорции. К примеру, нужно приготовить смесь в соотношении 1:40. Делите 1000 на 40, получаете 25. Столько миллилитров масла льёте на 1 литр бензина.

Решить пропорцию, как в школе. Для этого требуемый объём бензина в литрах делим на вторую цифру в пропорции. В результате получаем нужный объём масла в литрах. Переводим литры в миллилитры для удобства. Допустим, вам нужно 3 литра смеси в пропорции 1:50. Решаем: 3/50=0,06 л. Чтобы превратить литры в миллилитры, переносим запятую на три знака вправо, и получаем 60 миллилитров.
Посмотреть в таблице. Это самый простой, быстрый и наглядный способ, если пропорции стандартные. Остальные два способа нужны для того, чтобы понять, почему при пропорции 1:50 нужно лить на литр бензина 20 миллилитров масла, а не 50.

Пропорция	Масла на 1 л бензина (мл)
1:20	50 мл
1:25	40 мл
1:30	33 мл
1:35	28 мл
1:40	25 мл
1:45	22 мл
1:50	20 мл

Теперь кратко о том, почему у разных производителей отличаются пропорции и нет какого-то единого стандарта. На это есть, как минимум, три причины. Во-первых, разные характеристики масел и бензина. Во-вторых, качество сборки двигателей (технологии, материалы) тоже отличается. В-третьих, режим эксплуатации инструмента. К примеру, для обкатки бензопил некоторых производителей рекомендуется добавлять в смесь на 20% больше масла.

Пошаговая инструкция по заправке

Для приготовления топливной смеси и заправки бензопилы понадобится:

мерная ёмкость;
чистый бензин с октановым числом 92;
специальное масло для двухтактных моторов с воздушным охлаждением;
ёмкость для готовой смеси;
воронка.

Для измерения объёмов можно использовать ёмкость, которыми обычно комплектуются бензиновые инструменты. Также можно купить специальные фирменные канистры с отделами и мерными приспособлениями.

Пошаговая инструкция:

Приготовьте ёмкость для готовой топливной смеси. Её вместительности должно хватить и для бензина, и для масла.
Посчитайте пропорцию смазки и бензина, исходя из руководства по эксплуатации, и воспользовавшись одним из способов выше.
Отмерьте и налейте в ёмкость требуемый объём бензина.
При помощи мерного стакана, штатной бутылочки или шприца отмерьте и добавьте в бензин нужный объём масла.
Ёмкость для готовой смеси в итоге не должна быть полной под завязку.

Надёжно закройте ёмкость крышкой, и несколько раз переверните её для того, чтобы масло смешалось с бензином.
Заправьте приготовленную смесь в топливный бак бензопилы.

Вопреки гуляющему по Сети мнению, нет разницы, что первое заливать в ёмкость для приготовления смеси — бензин или масло. Главное, не забудьте тщательно перемешать. Вот чего на самом деле не стоит делать, так это готовить топливную смесь непосредственно в топливном баке бензопилы.

назад в блог

Задачи на пропорции по математике — примеры с ответами

Понятие пропорции

Чтобы решать задачи на тему пропорции, вспомним главное определение.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин.

Главное свойство пропорции:

Произведение крайних членов равно произведению средних.

a : b = c : d,

где a, b, c, d — члены пропорции, a, d — крайние члены, b, c — средние члены.

Вывод из главного свойства пропорции:

Крайний член равен произведению средних, которые разделены на другой крайний. То есть для пропорции a/b = c/d:
Средний член равен произведению крайних, которые разделены на другой средний. То есть для пропорции a/b = c/d:

Решить пропорцию — значит найти неизвестный член. Свойство пропорции — главный помощник в решении.

Запомним!

Равенство двух отношений называют пропорцией.

Рассмотрим легкие и сложные задачи, которые можно решить с помощью пропорции. 5, 6, 7, 8 класс — неважно, всем школьникам полезно проанализировать занимательные задачки.

Задачи на пропорции с решением и ответами

Свойства пропорции придумали не просто так! С их помощью можно найти любой из членов пропорции, если он неизвестен. Решим 10 задач на пропорцию.

Задание 1. Найти неизвестный член пропорции: x/2 = 3/1

Как решаем:

В этом примере неизвестны крайние члены, поэтому умножим средние члены и разделим полученный результат на известный крайний член:

x = (2 * 3)/1 = 6

Ответ: x = 6.

Задание 2. Найти неизвестный член: 1/3 = 5/y

Как решаем:

y = (3 * 5)/1 = 15

Ответ: y = 15.

Задача 3. Решить пропорцию: 30/x = 5/8

Как решаем:

x = (30 * 8)/5 = 48

Ответ: x = 48.

Задание 4. Решить: 7/5 = y/10

Как решаем:

y = (7 * 10)/5 = 14

Ответ: y = 14.

Задание 5. Известно, что 21x = 14y. Найти отношение x — к y

Как решаем:

Сначала сократим обе части равенства на общий множитель 7: 21x/7 = 14y/7.
Получим: 3x = 2y.
Теперь разделим обе части на 3y, чтобы в левой части убрать множитель 3, а в правой части избавиться от y: 3x/3y = 2y/3y.
После сокращения отношений получилось: x/y = 2/3.

Ответ: 2 к 3.

На следующем примере мы узнаем как составить пропорцию по задаче💡

Задание 6. Из 300 подписчиков в инстаграм 108 человек — поставили лайк под постом. Какой процент всех подписчиков составляют те, кому понравился пост и они поставили лайк?

Как решаем:

Примем всех подписчиков за 100% и запишем условие задачи кратко:
300 — 100%
108 — ?%
Составим пропорцию: 300/108 = 100/x.
Найдем х: (108 * 100) : 300 = 36.

Ответ: 36% всех подписчиков поставили лайк под постом.

Задание 7. Подруга Гарри Поттера при варке оборотного зелья использовала водоросли и пиявки в отношении 5 к 2. Сколько нужно водорослей, если есть только 450 грамм пиявок?

Как решаем:

Составим пропорцию: 5/2 = x/450.
Найдем х: (5 * 450) : 2 = 1125.

Ответ: на 450 грамм пиявок нужно взять 1125 гр водорослей.

Задание 8. Известно, что арбуз состоит на 98% из воды. Сколько воды в 5 кг арбуза?

Как решаем:

Вес арбуза (5 кг) составляет 100%. Вода — 98% или х кг.

Составим пропорцию:

5 : 100 = х : 98

х = (5 * 98) : 100

х = 4,9

Ответ: в 5 кг арбуза содержится 4,9 кг воды.

Перейдем к примерам посложнее. Рассмотрим задачу на пропорции из учебника по алгебре за 8 класс.

Задание 9. Папин автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Как рассуждаем:

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Обозначим:

v1 = 75 км/ч
v2 = 52 км/ч
t1 = 13 ч
t2 = х

Как решаем:

Составим пропорцию: v1/v2 = t2/t1.
Соотношения равны, но перевернуты относительно друг друга.

Подставим известные значения: 75/52 = t2/13
t2 = (75 * 13)/52 = 75/4 = 18 3/4 = 18 ч 45 мин

Ответ: 18 часов 45 минут.

Задание 10. 24 человека за 5 дней раскрутили канал в телеграм. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

Как рассуждаем:

1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.

2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.

3. Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:

Как решаем:

Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию:
30 : 24 = 5 : х

Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член:
х = 24 * 5 : 30
х = 4

Значит, 30 человек раскрутят канал за 4 дня.

Ответ: за 4 дня.

пропорция масла и бензина для бензопилы

Двигатель бензопилы — это «сердце» инструмента, поэтому очень важно использовать правильно приготовленную топливную смесь.

Топливная смесь для бензопилы готовится из двух составных — масла и бензина. Бензопилы оснащаются двухтактными двигателями, поэтому масло добавляется не в смазочную систему (как у четырехтактного двигателя), а непосредственно в бензин. При этом очень важно соблюдать верные пропорции ингредиентов и, конечно же, ни в коем случае не пытаться работать на чистом бензине, ведь таким образом, вы очень быстро «убьете» цепную пилу.

Масло обязательно должно быть предназначено для двухтактных двигателей садово-лесной техники (то есть ни в коем случае нельзя использовать масло для лодочных моторов или скутеров). Как показывает практика, такое масло можно купить в любом магазине или сервисном центре, где в продаже есть бензопилы или производиться их обслуживание.

Если говорить о том, какой бензин заливать в бензопилу, то оптимально будет использовать горючее с октановым числом А-95, в данном случае экономия на горючем может обернуться плачевно. Часто европейские производители указывают, что можно использовать бензин А-90 или А-92, но в постсоветских странах качество бензина уступает европейскому, поэтому в наших реалиях лучше использовать более качественный бензин.

Что касается самой пропорции бензо-масляной смеси, то здесь все просто: необходимо четко следовать инструкции к инструменту. Все производители бензопил указывают необходимое соотношение в руководстве по эксплуатации или в паспорте инструмента, кроме того, пропорции для заправки бензопилы могут отличаться в зависимости от модели цепной пилы. Как правило, пропорция масла и бензина к бензопиле именитых производителей это соотношение 1:40 или 1:50, что означает 1 часть масла на, например, 40 частей бензина.

Теперь арифметика — 1 л бензина = 1000 мл бензина, делим на 40 и получаем 25 мл масла. Если выполнить те же действия к соотношению 1:50, то получаем 20 мл масла на 1 л бензина.

Что касается бюджетных бензопил китайского производства, то ситуация немного иная. Соотношение бензина и масла для бензопилы made in China 1:25, то есть 1000 мл бензина делим на 25, получаем 40 мл масла. Все дело в том, что в фирменных бензопилах добротная сборка и расстояние между поршнями и цилиндрами в двигателе намного меньше, чем у китайских бензопил, поэтому и необходимое количество масла отличается практически в два раза.

Для того чтобы отмерить правильную порцию масла, воспользуйтесь обычным медицинским шприцем достаточного объема.

Еще одна тонкость — в сухую канистру для бензина сначала заливайте бензин, а потом масло. Процедура наоборот чревата топливной смесью низкого качества, ведь масло более плотное, прилипнет ко дну канистры. Поэтому о хорошем смешивания речь никак не может идти.

Обязательно готовьте топливную смесь в канистре и заливайте в бензобак уже готовое спецгорючее! Никогда не готовьте и не смешивайте ее непосредственно в топливном баке бензопилы!

Если с вопросом как разводить бензин для бензопилы разобрались, то и об условиях хранения и сроках годности топливной смеси стоит сказать несколько слов. Лучше всего и проще готовить бензомасленую смесь на 1 л бензина, делать это рекомендуется непосредственно перед работой с инструментом. Топливные баки бензопил имеют объем от 0,3 до 1 л. В условиях бытового использования за один сеанс редко используется весь объем приготовленной горючей смеси, поэтому остаток можно сохранить до следующего сеанса работы. Хранить топливную смесь необходимо в специальной канистре для бензина, в сухом темном месте. Оптимально рассчитывать, что срок хранения готовой смеси составит 7-10 дней

Дело в том, что масло представленное сейчас на рынке не синтетическое, а органическое, то есть натуральное. После 10 дней все смазочные свойства теряются, бензин попросту «съедает» масло. Естественно, использовать такое горючее уже нельзя, это может вызвать поломку и выход из строя бензопилы.

В конце работы необходимо слить топливную смесь и завести бензопилу — инструмент заглохнет (для того чтобы у пилы был сухой карбюратор) и теперь можно оставить ее до следующего сеанса эксплуатации.

Непригодную топливную смесь обязательно необходимо утилизировать!

Как варить рис рассыпчатым в кастрюле на воде

Рис является невероятно востребованным продуктом: из него готовят разнообразные гарниры и каши, заворачивают в роллы и добавляют в салаты, томят в плове и замешивают в ризотто. Он является ценным источником белка, витаминов, минералов и сложных углеводов. Но, несмотря на народную популярность, многие задаются вопросом — как варить рис, чтобы блюдо получилось вкусным?

Для того, чтобы в полной мере насладиться вкусом правильно приготовленного блюда, необходимо разобраться какой сорт риса является наиболее подходящим именно для него. Ведь каждый вид риса обладает своими уникальными достоинствами. Разберемся вместе!

На полках в магазине можно увидеть несколько различных видов риса MAKFA. Все они различаются временем варки, вкусом и способом использования в различных блюдах.

Универсальный рис длиннозерный

Традиционный и самый популярный рис продолговатой формы. Зернышки гладкие, ровные и немного прозрачные, длина варьируется от 5 до 8 мм. В процессе варки длиннозерный рис поглощает умеренное количество жидкости, поэтому остается рассыпчатым и сохраняет свою форму.

Что приготовить?

Такой рис идеально подавать на гарнир к любому мясу, птице и морепродуктам, добавлять в салаты, холодные закуски, в начинку для пирогов и пирожков.

Как варить рис на воде

Время приготовления: 15 минут.

Пропорции: 1 стакан риса — 2 стакана воды.

Выберите подходящий объем кастрюли из расчета того, что рис увеличится вдвое.
Промойте рис в холодной воде от 1 до 3 раз. Такая водная процедура позволит уменьшить количество крахмала и сделает готовый рис более рассыпчатым.
Залейте рис холодной водой, плотно закройте крышку и поставьте на максимальный огонь.
Как только вода закипит — посолите рис и перемешайте.
Плотно закройте крышку и убавьте огонь до минимума. Постарайтесь «не беспокоить» рис: не поднимать крышку и не выпускать образовавшийся пар.
Варите рис в течение 20 минут.

Ароматные травы, такие как орегано и тимьян сделают гарнир из риса более необычным и привлекательным. Для получения насыщенного аромата добавляйте их в кипящую воду за 5 минут до готовности.

Нежный рис круглозерный

Белоснежный рис с плавными и округлыми краями, зернышки длинной не более 5 мм. Этот сорт является самым крахмалистым и в процессе варки в кастрюле впитывает большое количество жидкости, поэтому хорошо разваривается и склеивается. Сварить круглозерный рис рассыпчатым невозможно, поэтому используйте его исключительно для нежных кремообразных блюд.

Что приготовить?

Рис превосходно проявляет свои качества в приготовлении сладостей: в кашах, пудингах и молочных супах. Благодаря высокой клейкости отлично подходит для приготовления ризотто, суши, ежиков и тефтелей.

Как варить круглозерный рис на воде

Время приготовления: 15 минут.

Пропорции: 1 стакан риса — 2 стакана воды.

Выберете подходящий объем посуды из расчета того, что рис увеличится втрое.
Засыпьте рис в кастрюлю, залейте холодной водой и поставьте на максимальный огонь.
Дайте воде закипеть и добавьте немного соли.
Убавьте огонь, варите, не помешивая и не открывая крышки.
По прошествии 15 минут снимите кастрюлю с огня и оставьте томиться под полотенцем еще на 10 минут.

Если хотите отварить рис для суши, его следует предварительно замочить в холодной воде на 30 минут. Так крупа станет мягче и податливее при формировании нужной формы.

Рассыпчатый рис обработанный паром

Современная технология обработки зерна паром позволяет получить уникальный рассыпчатый рис, который в готовом виде выглядит как «рисинка к рисинке». Зернышки такого риса не слипаются и сохраняют четкие контуры даже при повторном разогревании блюда. Благодаря пару зерно становится тверже и приобретает янтарный оттенок.

Что приготовить?

Используйте его в азиатских блюдах и любой вариации плова с мясом или овощами.

Как варить рис рассыпчатым в кастрюле

Время приготовления: 25 минут.

Пропорции: 1 стакан риса — 2,5 стакана воды.

Выберете подходящую посуду: это должна быть кастрюля с толстым дном, казан или тажин. Не стоит использовать эмалированные кастрюли, так как в них рис может пригореть и испортить аромат блюда.
Промойте рис один раз для удаления лишнего крахмала.
Залейте рис холодной водой и варите на медленном огне в течение 20 минут, не перемешивая и не поднимая крышки.
Не удивляйтесь, если в процессе варки пропаренный рис поменяет свой цвет с янтарного на белоснежный, это нормально.

Рис, обработанный паром, имеет большое преимущество перед другими видами риса: он сохраняет до 80% витаминов и минералов, содержащихся в оболочке зерна.

Практичный рис в пакетиках для варки

Рис в пакетиках очень удобен при варке: он не пригорает ко дну и стенкам кастрюли, его не нужно промывать и отмерять нужное количество воды. Как правило, такой рис уже разделен на порции в индивидуальных пакетиках.

Как варить рис на гарнир

Время приготовления: 15-25 минут (указывается на упаковке).

Пропорции: 1 пакетик риса — 1 литр воды.

Вскипятите в кастрюле необходимое количество воды.
Встряхните пакетик и равномерно распределите зерна по поверхности.
Добавьте в воду соль и опустите пакетик с рисом.
Проконтролируйте, чтобы вода полностью покрывала пакетик в течение всего времени приготовления.
После окончания варки не оставляйте рис в горячей воде, сразу извлеките пакетик, оторвите край по линии отрыва и сервируйте блюдо.

Хитрости опытных хозяек

Трюк с полотенцем

Используйте чистое кухонное полотенце чтобы сохранить идеальную рассыпчатость риса и не допустить попадание лишней жидкости. Просто поместите его под крышку за пять минут до готовности. Ткань соберет весь лишний конденсат с крышки и не позволит рису стать влажным.

Капелька масла

Добавьте столовую ложку растительного масла в кипящую воду, в которой планируете варить рис. Это остановит выделение крахмала и позволит получить отдельные зернышки, которые эффектно смотрятся в салатах и закусках.

Тонкий ореховый аромат

Предварительно обжарьте рис в небольшом количестве масла. Сделать это можно прямо в кастрюле, в которой будет готовиться блюдо. Просто высыпьте сухой рис и обжаривайте его в течение 5 минут до слегка золотистого цвета. Добавьте воду и готовьте как обычно. Изменения будут очень тонкими, но это хватит чтобы оживить будничное блюдо.

Желтый или белый

Для того, чтобы рис приобрёл аппетитный желтый оттенок, добавьте в воду треть чайной ложки куркумы. А если хотите получить идеальный белоснежный цвет, то капельку лимонной кислоты или уксуса.

Готовим вместе с MAKFA

MAKFA производит и фасует исключительно качественные крупы для ежедневного потребления. Производственная площадка, расположенная на Алтае, оснащена самым современным оборудованием, которое позволяет ежедневно выпускать несколько тысяч тонн продукции для любимых покупателей по всей России и странам СНГ.

Чередуя различные виды риса, представленного в ассортименте компании MAKFA, вы сможете составить разнообразное и полезное меню для своей семьи.

Попробуйте приготовить:

Ризотто с грибами

Голубцы с рисово-овощной начинкой

Узбекский плов

Рисовую кашу с апельсиновым сиропом

Греческую мусаку с баклажанами

Просто о саженях и золотой пропорции — портфолио графического дизайнера Артёма Владимирова

Предисловие

Приветствую, Человек!
Великий Google привёл вас на эту страницу, а значит вас интересуют серьёзные темы. В этой статье я покажу, как рождается число Φ, где прячется золотая пропорция и как она применима. А также научу умножать и делить на два. Весь материал является размышлениями на заданную тему — на абсолютную истину не претендует. Призываю вместе проверить всё написанное, математика и геометрия дадут нам ключ. Все желающие приглашаются к обсуждению по электронной почте.

Наверняка вы уже имеете какое-то представление о Золотом сечении, здесь я не буду подробно останавливаться на историческом и культурном аспектах — в Интернете полно информации об этом. Здесь я хочу изучить этот феномен с помощью точной науки — математики.

§1. Начало. Ряд Фибоначчи

Запишем ряд чисел, начиная с единицы, в котором каждое следующее число является суммой двух предыдущих. Найдём соотношение (пропорцию) каждой пары соседних чисел друг другу, поделив следующее на предыдущее.

1 + 1 = 2;
1 + 2 = 3;
2 + 3 = 5;
3 + 5 = 8;
5 + 8 = 13;
8 + 13 = 21;
13 + 21 = 34;
21 + 34 = 55;
34 + 55 = 89;
55 + 89 = 144.
1 : 1 = 1;
2 : 1 = 2;
3 : 2 = 1,5;
5 : 3 = 1,667;
8 : 5 = 1,619;
13 : 8 = 1,618;
21 : 12 = 1,618;
34 : 21 = 1,618;
55 : 34 = 1,618;
89 : 55 = 1,618.

1 1 2 3 5 8 13 21 34 55 89

На шестой паре чисел появляется постоянное соотношение 1,618, которое остаётся неизменным до бесконечности, что само по себе уже интересно. Ряд может начинаться с любой пары чисел и соотношение всегда выравнивается до 1,618.

§2. Число Фи

1,618033988749894848045…

Φ — бесконечное иррациональное число. Но для наших примеров нам такая точность не нужна, достаточно 1,618.

Число Φ вычисляется по формуле (1 + √5) : 2

§3. Золотое сечение

Золотое сечение определяют как отношение меньшего отрезка к большему отрезку как отношение большего к их сумме:

a : b = (a + b) : a

a + b

Термин «Золотое сечение» я считаю не совсем корректным, не отражающим процесс.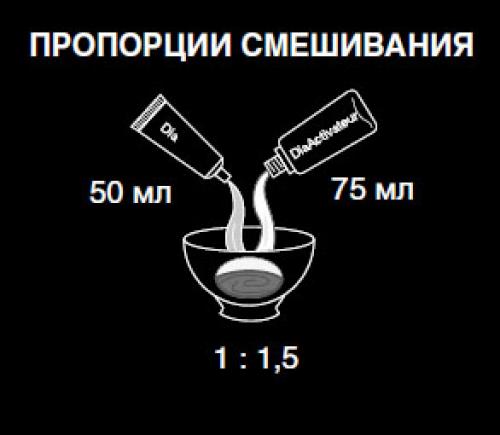 По-английски golden ratio дословно: золотое соотношение. Более уместен термин «Золотая пропорция».

§4. Метрическая система

Метр — длина пути, проходимого светом в вакууме за интервал времени 1/299 792 458 секунды

Так гласит официальное определение метра, принятое XVII Генеральной конференцией по мерам и весам в 1983 году. Метр был введён в СССР 14 сентября 1918 указом СНК РСФСР «О введении международной метрической десятичной системы мер и весов».

Расстояние, пройденное светом за одну трехсотмиллионную долю секунды. Вам это ясно? Как это применять в обычной жизни? Как проектировали и строили сооружения в более ранние века? Неужели мужик, строя дом, будет руководствоваться иррациональными числами и вычислять квадратные корни? Конечно же нет. Очевидно, что существовала другая система мер, и её отголоски сохранились в Королевской системе мер, а также в русских саженях. Нужен простой и понятный инструмент пропорционирования и соизмерения.

§5. Пропорции квадрата

Мы знаем, что у квадрата все стороны равны. А это значит, что квадрат можно нарисовать или построить, имея в руках лишь одну меру любой длины: карандаш, палку и т.д. Примем его сторону за единицу.

Диагональ квадрата — редко используемая величина, но и она весьма полезна и интересна (рис. 1).
По теореме Пифагора длина диагонали квадрата (она же гипотенуза треугольника) равна корню из суммы квадратов катетов:

√ (1·1+1·1) = √2 = 1,4142

Пропорцию 1 : √2 также называют серебряным сечением. Самый известный пример этой пропорции — лист формата А4. Эта пропорция обладает интересным свойством, что сохраняется неизменной при удвоении какой-либо из сторон.

Что собой представляет корень из пяти √5 в формуле Φ = (1 + √5) ÷ 2? Это всего навсего диагональ двух квадратов (рис. 2)! Проверим по теореме Пифагора:

√ (1·1+2·2) = √5 = 2,236

Суммируем величину стороны квадрата (1) и диагональ двух квадратов (2,236). Поделим пополам и получим число Φ. Получается, что длина стороны квадрата и длина диагонали двух квадратов в сумме равны удвоенному числу Φ (рис. 3)!

Φ = 3,236 : 2 = 1,618

Удвоенный квадрат по своей сути также является половиной квадрата большего размера. А значит √5 — это также диагональ половины квадрата, а число Φ можно получить, опустив диагональ половины квадрата на продолжение его стороны (рис. 4).

Квадрат хранит число Φ

Нам не нужно знать иррациональные числа, математика лишь подтверждает расчёты, но не является их основой! Квадрат хранит в себе все нужные нам пропорции. Он инструмент пропорционирования! Умножая эти пропорции квадрата на целый коэффициент, мы можем получить пропорциональные величины любой нужной длины.

Построение прямоугольника в пропорции Золотого сечения

§6. Интересные превращения числа Φ

Теперь стало понятно, где прячется число Φ, я покажу, как оно меняется с точки зрения математики — здесь очень много волшебных превращений! Все они пригодятся нам в дальнейшней работе с саженями.

1). Если от Φ отнять единицу, получится тоже самое, если единицу поделить на Φ:

Φ − 1 = 1 ÷ Φ = 0,618

2). Если из двух Φ вычесть диагональ двух квадратов, получим единицу (рис. 2, 4):

2Φ − √5 = 1,000

3). Помним, число Φ равно половине суммы стороны квадрата и диагонали двух квадратов:

Φ = (1 + √5) ÷ 2 = 1,618

4). Если Φ умножить на диагональ двух квадратов минус единица, будет 2:

Φ · (√5 − 1) = 2,000

5). Если к Φ прибавить единицу, получится тоже самое, если Φ умножить само на себя:

Φ + 1 = Φ² = 2,618

6). Если к Φ прибавить двойку, получится тоже самое, если Φ умножить на диагональ двух квадратов:

Φ+2 = Φ²+1 = Φ·√5 = 3,618

7). Если двойку поделить на Φ получится тоже самое, если из 2Φ вычесть два:

2 ÷ Φ = 2Φ − 2 = 1,236

8). Если из 2Φ вычесть единицу, получим диагональ половины квадрата (рис. 2, 4):

2Φ − 1 = √5 = 2,236

9). Если удвоить любым способом Φ, получим 1 + √5 или 2Φ (рис. 3):

2Φ = 1 + √5 = 3,236

10). Если возвести Φ в куб, получим 2 + √5, а это две стороны квадрата + диагональ двух квадратов:

Φ³ = 2 + √5 = 4,236

Трудно не заметить, две группы чисел с одинаковыми знаками после запятой, и это не спроста!

§7. Система пропорций

Возвращаясь к Золотой пропорции. Суть вовсе не в том, что какой-то отрезок делит какой-то другой. Недостаточно нарисовать спираль улитки поверх фото, чтобы понять, что это означает и как этим пользоваться. Для работы на плоскости нужно два отрезка, а для построения объёма нужны три!

1 — 1,236 — 1,618

Появляется система пропорций 1 : 2÷Φ : Φ, которую уже можно использовать как коэффициенты при соизмерении. Рабочая система состоит из трех отрезков и выглядит так:

1,236

1,618

§8. Образ, подобие, мера и каравай

С математекой, должно быть ясно. Вспомним, что мы, человеки, созданы по образу и подобию Бога, или нашего Создателя, или Вселенной, или Природы, или чего-либо ещё. Оставим религиозные смыслы и обратимся к геометрии. Подобными в ней назвают фигуры одинаковых геометрических пропорций и свойств. Квадраты, круги и равносторонние треугольники всегда подобны таким же фигурам. А раз мы уже нашли золотую пропорцию в числах Фибоначии и в квадрате, давайте искать её в самих себе!

Тело человека уже хранит в себе образ и подобие — Золотую пропорцию!

Вспоминим русскую народную песенку про каравай:

Как на наши именины испекли мы каравай,
Вот такой вышины (поднимаем руки вверх)
Вот такой нижины (опускаем руки вниз)
Вот такой ширины (раскидываем руки вширь)
Вот такой ужины (сводим руки вместе)
Каравай, каравай, кого любишь выбирай!
Я люблю, конечно, всех, но вот (этих) — больше всех.

Какие движения при этом делают дети? Водят хоровод и показывают руками вышину, нижину, ширину и ужину! Проделайте сами те же движения и вы сразу поймёте, какими мерами показывают высоту, ширину и длину. Эта песенка и есть ключ!

Ключ к системе измерений саженями хранится в русской народной культуре! В простой детской песенке, которую знают все с малых лет. Мерить всё по себе — это правильно, логично и само собой разумеется! Однако, теперь это признак эгоизма — выбросим этот нонсенс из своей головы.

§9. Золотая пропорция тела человека

Рука вверх — это мера высоты (великая сажень),
Размах рук в стороны — это мера ширины (маховая сажень),
Рука вперёд — это мера длины (полсажени длины).

Эти меры являются вашими личными мерами!

Все три меры образуют единую систему соизмерений на основе пропорции 2÷Φ к 1. Разные измерения (длина, ширина, высота) должны мериться своей соответствующей мерой, то есть саженью. И тогда мы можем забыть об иррациональных числах, корнях и прочем, используя вместо них целые количества своих саженей.

§10. Казённая сажень отдельно

Важно отметить, что вопреки официально утверждённой казённой сажени, существовали и другие. И лишь она одна была приравнена к 7 английским футам и позже к 213 см в Российской империи и по другим источникам 218 см в СССР. На то она и являлась казённой. В корне неверно считать, что сажень была одна, как метр. Чтобы понять гармонию, не думайте о метре — это изобретение XIX века, а Вселенная со своими пропорциями вечна. 🙂

§11. Погрешность измерений

Я намеренно буду округлять сотые и тысячные доли чисел и подтягивать расчёты под единый вид, так как они заведомо не абсолютно точны. Иррациональные числа не делятся до конца, поэтому не везде удастся получить красивые целые числа. А мы должны увидеть картину в целом, понять всю единую систему, где тысячные доли лишь детали.

Сантиметр — это сотая доля метра, достаточно точно, поэтому предлагаю не использовать миллиметры в своих расчётах, чтобы они не создавали лишний шум. К тому же, тело гибкое и руки можно растянуть ещё шире или поднять ещё выше. Этого делать не нужно, положение должно быть комфортным.

§12. Измерим себя и проверим

Пора проверить всё на себе и удивиться, что всё так и есть. Я мужчина среднего роста, мой размах рук примерно 188 см. Высота поднятой руки примерно 232,5 см. Вытянутая рука вперёд (плюс столько же назад) примерно 152 см. Сначала я измерил всё рулеткой, а потом посчитал на калькуляторе. Меня поразило с какой точностью совпали все цифры.

188 / 152 = 1,236
152 / 188 = 0,809
232,5 / 188 = 1,236
188 / 232,5 = 0,809
232,5 / 152 = 1,529
152 / 232,5 = 0,655

Здесь мы видим четыре любопытных числа. Где же здесь число 1,618? Да вот же оно:

1,236 = 2 ÷ Φ

0,809 = Φ ÷ 2

1,528 = (2 ÷ Φ)²

0,655 = Φ² ÷ 4

Опишем это словами, чтобы появилось понимание, что всё это значит. Поделив сажень высоты на сажень ширины мы получим пропорцию 1 к 2 ÷ Φ, точно также как поделив сажень ширины на сажень длины. Если поменять местами величины, получится пропорция 1 к Φ ÷ 2. Пропорции остаются одинаковы. А значит мы можем подставлять сюда любые величины и любые значения в сантиметрах!

2 ÷ Φ / 1 = 1,236; делим большее на меньшее
1 / 2 ÷ Φ = 0,809; делим меньшее на большее

Калькулятор саженей

Чтобы посчитать ваши личные сажени, введите величину размаха рук в см:

0 см

Январь 2019. Продолжение следует.

Другие статьи

Таблица пропорций и марок бетона на 1м3

Качественный бетон получается благодаря правильным пропорциям. Основными элементами раствора являются песок, щебень, цемент. Пропорции помогают создать надежный бетон, найти правильное соотношение элементов в составе. Изготавливать раствор на глаз не рекомендуется, получится плохое качество строительного материала. Придерживаясь рекомендаций, выйдет бетон необходимой прочности.

Марка бетона . . . . . . . . . . . . . . М100
Пропорции марки на 1м3 . . . 1 : 5,8 : 8,1
Цемент (М500) . . .. . . . . . . . . . 1 кг
Песок . . . . . . . . . . . . . . . . . . . . . 5,8 кг
Щебень . . . . . . . . . . . . . . . . . . . 8,1 кг

Марка бетона . . . . . . . . . . . . . . М150
Пропорции марки на 1м3 . . . 1 : 4,5 : 6,6
Цемент (М500) . . .. . . . . . . . . . 1 кг
Песок . . . . . . . . . . . . . . . . . . . . . 4,5 кг
Щебень . . . . . . . . . . . . . . . . . . . 6,6 кг

Марка бетона . . . . . . . . . . . . . . М200
Пропорции марки на 1м3 . . . 1 : 3,5 : 5,6
Цемент (М500) . . .. . . . . . . . . . 1 кг
Песок . . . . . . . . . . . . . . . . . . . . . 3,5 кг
Щебень . . . . . . . . . . . . . . . . . . . 5,6 кг

Марка бетона . . . . . . . . . . . . . . М250
Пропорции марки на 1м3 . . . 1 : 2,6 : 4,5
Цемент (М500) . . .. . . . . . . . . . 1 кг
Песок . . . . . . . . . . . . . . . . . . . . . 2,6 кг
Щебень . . . . . . . . . . . . . . . . . . . 4,5 кг

Марка бетона . . . . . . . . . . . . . . М300
Пропорции марки на 1м3 . . . 1 : 2,4 : 4,3
Цемент (М500) . . .. . . . . . . . . . 1 кг
Песок . . . . . . . . . . . . . . . . . . . . . 2,4 кг
Щебень . . . . . . . . . . . . . . . . . . . 4,3 кг

Марка бетона . . . . . . . . . . . . . . М350
Пропорции марки на 1м3 . . . 1 : 1,9 : 3,6
Цемент (М500) . . .. . . . . . . . . . 1 кг
Песок . . . . . . . . . . . . . . . . . . . . . 1,9 кг
Щебень . . . . . . . . . . . . . . . . . . . 3,6 кг

Марка бетона . . . . . . . . . . . . . . М400
Пропорции марки на 1м3 . . . 1 : 1,6 : 3,2
Цемент (М500) . . .. . . . . . . . . . 1 кг
Песок . . . . . . . . . . . . . . . . . . . . . 1,6 кг
Щебень . . . . . . . . . . . . . . . . . . . 3,2 кг

Марка бетона . . . . . . . . . . . . . . М450
Пропорции марки на 1м3 . . . 1 : 1,1 : 2,5
Цемент (М500) . . .. . . . . . . . . . 1 кг
Песок . . . . . . . . . . . . . . . . . . . . . 1,1 кг
Щебень . . . . . . . . . . . . . . . . . . . 2,5 кг

Подходящие марки бетона

Количество добавок зависит от марки бетона, она показывает прочность строительного материала. Все расчеты проводятся по соотношению на 1М3. Состав любой марки требует наличия цемента М500, в количестве один килограмм. Остальные элементы добавляются в разных размерах. Бетон класса М100 требует 6 кг песка, 8 килограммов щебеня. Требуется тщательно перемешивать раствор, следить за его консистенцией.

Марка М150 состоит из 4 килограммов песка, 6 кг щебня. Похожие пропорции имеет класс М200. Раствор содержит 3,5 килограмма песка, 5,5 кг щебня. Популярный класс бетона М250 включает:

Цемент М500 (применяется для всех марок бетона).
Песок – 2,6 килограмма.
Щебень – 4,5 кг.

Класс М300 используется для строения различных строений, состав содержит песок 2,4 килограмма, щебень 4,3 килограмма. Меньше затрат у марки бетона М350. Необходимо добавить к цементу два кг песка, 3,6 килограмм щебня. Класс М400 содержит 1,6 килограмма песка, 3,2 кг щебня. Последняя марка бетона – М450. Раствор изготавливается из одного килограмма песка, 2,5 килограмма щебня.

Заказать качественный бетон в компании «Бетонная индустрия»

Купить бетон с доставкой поможет компания «Бетонная индустрия». Фирма изготавливает любые марки строительных материалов на собственном производстве. Используется современное оборудование, готовый бетон проверяется на качество, прочность. Приемлемые цены позволяют сэкономить денежные средства. Продаем бетон для строительства, кладки, штукатурки.

Гарантируем высокое качество продукции, доставка осуществляется специальной техникой, присутствует собственный автопарк. Оформить заявку можно онлайн, используя официальный сайт организации. Заказать товар предлагается и по телефону горячей линии +7 (925) 450-11-97.

Таблица «Пропорции бетона на 1м3». Качественные бетонные смеси

ПОДЕЛИТЕСЬ
В СОЦСЕТЯХ

Ни одна площадка промышленного и жилого строительства не обходится без использования бетона. Качество этого искусственно полученного материала напрямую зависит от последовательности смешивания и соотношения используемых компонентов. Таблица «Пропорции бетона на 1м3» сориентирует в максимально правильном распределении составных частей раствора для использования его в тех или иных конструкциях.

В зависимости от предназначения, могут использоваться различные пропорции приготовления бетонного раствора

Технические характеристики бетона

Цемент и вода, входящие в состав бетона, образуют при смешивании массу, которая, затвердевая, превращается в цементный камень. В таком виде этот материал легко деформируется, в нем образуется множество микротрещин, что приводит к значительной усадке.

Добавление в состав цементной смеси наполнителей (щебня, песка, гравия и др.) способствует образованию своеобразной арматуры, которая принимает на себя внутреннее напряжение. Благодаря этому улучшаются показатели прочности, ослабевает подвижность смеси и деформация от усадки.

Различные наполнители придают бетону прочность и увеличивают его технические характеристики

Учитывая степень прочности бетона, материал делится на классы (обозначается «В») и марки (обозначается «М»). Чем выше числовые значения марок бетона (например, М200, М300 или М400), тем более прочным считается материал. От класса и марки зависит, в каких видах конструкций он будет применяться.

Если строительство вашего объекта подкреплено проектом, то в нем уже предопределены марки бетона, необходимые для устройства фундамента или других конструкций.

Таблица показателей прочности бетона:

Марка бетона	М75	М100	М150	М200	М250	М300	М350	М400
Нагрузка (нормативная), кгс/см²	65	98	131	196	262	294	327	393

Соответствие марки применению бетона

Бетонные смеси с разными марками используются для разнотипных сооружений.

В таблице приведена сфера возможного использования бетона в зависимости от марки:

Марка М100-М150	Марка М200-М250	Марка М300	Марка М350	Марка М400
Основа (подложка) под стяжку, фундамент, плитку или дорожку из бетона.	Фундаменты одноэтажных зданий, стяжка, отмостка, площадки, лестницы.	Ленточные фундаменты, монолитные стены, стяжка, отмостка, площадки, лестницы.	Отливка ж/б конструкций (балки, опорные колонны, ригеля, перемычки, плиты перекрытий, бассейны).	Гидросооружения (дамбы, мосты), фортификационные объекты (бункеры, хранилища).

Расход и пропорции основных ингредиентов бетона зависит от многих факторов. Что касается песка, то следует учитывать его влажность, крупность, содержание примесей. Для щебня и гравия имеет значение показатели влажности, загрязнения, пустотности, нестандартных включений (мусора).

Для цемента учитывается его марка. Также учитывается вид работ, для которых готовится бетонный раствор: бетонная стяжка, заливка фундамента, возведение стен и др.
Основная составляющая бетонного раствора — цемент. Соотношение расхода этого материала выражает марку бетона. Марка бетона выше, чем больше в его составе цемента.

Для приготовления бетонной смеси используются различные марки цемента

Традиционно бетонирование производят в период, когда температура воздуха имеет плюсовое значение. Это способствует качественному затвердеванию раствора.

Полезный совет! Не рекомендуется выполнять бетонные работы при отрицательных температурах, ввиду возможной вероятности получения некачественного по прочности материала.

Работая с бетоном в холодный период года есть вероятность, что вода в составе раствора заледенеет и станет источником разрушения внутри материала. Таким образом, снизится прочность.

Схватывание бетона происходит в период 12 ч, в двухнедельный срок бетон накапливает 80% прочности. Эксплуатация готовой конструкции становится возможной через месяц.

Испытание готовой бетонной конструкции на скалывание с помощью специального прибора

Основные компоненты бетонной смеси

Приобретая составные ингредиенты для приготовления раствора, убедитесь (насколько возможно) в их качестве:

вода: применяется пресная;
песок: не должен в своем составе содержать глину, визуально проверить можно по цвету. Если песок желтого насыщенного цвета — значит содержание глины в нем велико. Для раствора используется белый или серый песок;
цемент: на ощупь мешки с цементом не должны иметь затвердевшие части и материал должен быть изготовлен не раньше четырех месяцев от даты приобретения;

Полезный совет! Приобретая цемент, обращайте внимание на маркировку. Только у проверенных производителей маркировка на мешке соответствует качеству содержащегося в нем цемента.

Цемент — первая и главная составляющая бетонного раствора

щебень: используется чистый материал, без пыли и других включений. В противном случае сцепление с раствором будет недостаточным, что негативно скажется на прочности бетона. Идеально подойдет щебень гранитной породы;
кроме щебня, в качестве крупного наполнителя для бетонной смеси, используют гравий (обычно применяется для марки 450), известняк (подходит для марок 100 и 300), гранит (отличается прочностью, морозоустойчивостью и низким поглощением воды).

Для приготовления смеси используют чистый щебень, без загрязнений и посторонних примесей

Расход материалов. Таблица «Пропорции бетона на 1м3»

Расходование компонентов для приготовления 1м³ бетона напрямую зависит от назначения конструкций и марки цемента, участвующего в изготовлении. Для этого обобщили значения пропорций состава 1м³ бетона.

Ниже представлены две таблицы пропорций бетона на 1м3.

Таблица №1 — пропорции бетона для марок М100, М200, М400 и М400:

Марки бетона: М100, М200, М300, М400

Таблица №2 — пропорции бетона для марок М150, М250, М350 и М450:

Марки бетона: М150 — М450

Таким образом, если необходимо произвести бетон М200, пропорции будут составлять на
1 м³ раствора — 1 / 3,5 / 2,6 (кг), для бетона М300, пропорции составят — 1 / 2,4 / 4,3 (кг), пропорции бетона М400 — 1 / 1,6 / 3,2 (кг).

Для примера можно рассчитать количественный состав компонентов, учтенных таблицей пропорций для приготовления бетона М400 с использованием цемента М500. Возьмем 20 ведер цемента. Песок по пропорциям будет составлять (20 х 1,6) = 32 ведра. Щебень соответственно — (20 х 3,2) = 64 ведра. И вода — (20 х 0,5) = 10 ведер. Зная плотность всех компонентов можно легко перевести требуемое количество ведер в те единицы измерения, по которым происходит реализация материалов. Так, ведро емкостью 10 литров, наполненное цементом, будет весить 12 кг (10 х 1200), где 1200 кг/м³ — плотность цемента при насыпании, ведро песка — 14 кг (10 х 1400), где 1400 кг/м³ — плотность песка, такой же объем гравия будет весить 15 кг, учитывая его плотность.

Заливка ленточного фундамента бетонной смесью

Пропорции состава бетона для фундамента

Если бетонные работы производятся в малых объемах, например, при частном строительстве или разовых мелких работах, целесообразно придерживаться пропорций бетона в ведрах. Такие количественные меры применяются, если нет возможности расположить на строительном участке специальную технику, а также когда раствор заливают небольшими порциями.

При производстве бетона под конструкцию фундамента, необходимо придерживаться следующих пропорций бетона на фундамент, приведенных ниже.

Таблица пропорций бетона на фундамент в ведрах, для марок М100, М200, М300 и М400:

При использовании цемента марки 400 и 500 на объем 10 литров

Порядок приготовления раствора

В условиях индивидуального строительства бетонный раствор для фундамента готовят, отмеряя части компонентов ведрами. Следует учитывать, что ведро и лопата для цемента должны быть исключительно сухими. Для получения более точных пропорций, состав песка и щебня в ведре немного уплотняют и ровняют по краю ведра. Отмеренные щебень с песком хорошо перемешивают в удобной широкой таре, формируя канавки, куда высыпают подготовленный цемент. Все ингредиенты (количество которых подобрано из таблицы пропорций) изрядно перемешивают до получения равномерной по цвету массы.

Статья по теме:

Сколько весит куб бетона? Основные характеристики и состав. Определение веса. Разновидности бетонов в зависимости от материала. Виды бетонов (легкие и тяжелые). Что влияет на вес бетона?

Полученную массу формируют под конус, в середине устраивают углубление, куда и заливают воду. Постепенно ссыпают смесь с краев в середину, пока вода полностью не впитается. Как только первая порция воды пропитается, процедуру с водой повторяют до образования нужной консистенции бетонного раствора.

Приготовление цементного раствора своими руками путем замешивания

Полезный совет! Не рекомендуется нарушать водоцементное отношение, стремясь получить более жидкий раствор. Избыток воды будет оставлять пустоты, в результате чего уменьшится прочность бетона.

Придерживаясь таблицы пропорций приготовления бетона, можно получить состав из однородной, пластичной смеси. Это послужит залогом прочности и долговечности бетона в эксплуатации.

Выполнение технических норм в приготовлении бетонных смесей способствует сохранению основных показателей, необходимых в строительстве.

СМОТРИТЕ ТАКЖЕ

Проверка пропорциональности | Purplemath

Purplemath

В теме пропорций есть определенная терминология, которую вам, возможно, нужно знать. Например, учитывая следующее уравнение пропорции:

… значения в позициях « b » и « c » называются «средними» пропорциями, а значения в позициях « a » и « d » называются «крайности» пропорции.

Основным определяющим свойством любой пропорции является то, что произведение средних значений равно произведению крайностей. Другими словами, учитывая пропорциональную формулировку:

MathHelp.com

…. мы знаем, что это должно быть правдой, что г. до н.э. равно г. до н.э. г. Этот факт о пропорциях, по сути, является перекрестным умножением, продемонстрированным на предыдущей странице. И этот факт перекрестного умножения о произведениях средних и крайностей иногда превращается в домашнюю задачу, например:

Пропорционально ли
²⁴/₁₄₀ ³⁰/₁₇₆? Объясните, почему (или почему нет), не упрощая дроби.

Чтобы эти дроби (то есть эти отношения) были пропорциональны (то есть, чтобы они создавали истинное пропорциональное уравнение, когда они устанавливаются равными друг другу), должно быть верно, что произведение средних значений этого уравнения равно произведению крайностей. Итак, я могу выяснить, действительно ли две фракции пропорциональны друг другу (не упрощая их), найдя эти два продукта.

Другими словами, указав, что я должен , а не , упростить дроби, они намекают, что хотят, чтобы я нашел произведение 140 и 30 (это означает, что если я сохраню дроби в том же порядке как они дали их мне) и произведение 24 и 176 (являются крайними значениями), а затем посмотрите, равны ли эти продукты.Так что проверю:

140 × 30 = 4200

24 × 176 = 4224

Хотя эти значения близки, они не равны, поэтому я знаю, что исходные дроби не могут быть пропорциональны друг другу. Итак, мой ответ:

Дроби не пропорциональны, потому что произведение их средних не равно произведению их крайних значений.

Если бы я поменял местами дроби и использовал 176 и 24 как мои средние, а 30 и 140 как крайние значения, я бы получил те же продукты (только в обратном порядке) и, таким образом, тот же ответ (а именно, что дроби не пропорциональны).Так что не беспокойтесь о том, какая дробь является «первой» или «второй»; в любом случае будет работать.

Является ли 42/55 пропорциональным 50/65? Обоснуйте свой ответ, не уменьшая дробей.

Чтобы подтвердить пропорциональность (или опровергнуть ее), мне нужно установить пропорцию, умножить средние, умножить крайности и сравнить результаты. Или, что то же самое (но без выполнения уравнения, которое на самом деле может быть неверным), я умножу знаменатель одной дроби на числитель другой, и наоборот:

(42) (65) = 2,730

(55) (50) = 2,750

И снова они близки, но не равны.Итак:

Дроби не пропорциональны, потому что произведение их средних не равно произведению их крайних значений.

Пропорциональны ли 42/273 и 170/1105? Объясните свой ответ, не сокращая дроби и не переводя их в общий знаменатель.

Я «перемножаю» (в данном контексте означает умножение числителя одной дроби на знаменатель другой, и наоборот):

(42) (1,105) = 46 410

(273) (170) = 46 410

Наконец, пара пропорциональна !

Дроби пропорциональны, потому что, когда они установлены как пропорции, произведение средних равно произведению крайних значений.

Средние пропорции

Другой технический тип упражнения, основанный на терминологии пропорций, — это нахождение «среднего пропорционального» между двумя числами. Средние пропорциональные — это особый класс пропорций, где средние пропорции равны друг другу. Пример среднего пропорционального будет:

В уравнении пропорциональности, созданном этими двумя равными дробями, средние значения пропорции имеют одно и то же значение, «2», а крайние значения — 1 и 4.Это говорит нам о том, что число 2 является «средним пропорциональным» между числами 1 и 4.

В упражнениях, основанных на пропорциональном среднем, нам могут дать два значения и попросить найти среднее пропорциональное между ними.

Найдите среднее значение, пропорциональное 3 и 12.

Они дали мне два числа и ключевое слово «среднее пропорциональное».Итак, я знаю, что мне нужно установить пропорцию, используя заданные значения в качестве крайних значений, а затем я должен найти средства.

По определению «среднее пропорциональное» я знаю, что средним будет одно и то же значение. Я позволю « x » быть тем единственным значением, которое я ищу. Я составлю уравнение пропорции, используя свою переменную в качестве средних и два значения, которые они дали мне в качестве крайних значений:

Теперь я произведу перекрестное умножение и решу для значения x :

3 × 12 = x ²

36 = x ²

± 6 = х

Поскольку я ищу среднее пропорциональное 3 и 12, я бы подумал, что мне нужно будет взять только положительное значение в качестве ответа, так что среднее пропорциональное будет как раз 6.Однако с учетом дробей подойдет любое значение:

Если я проверю перекрестные произведения каждого уравнения, я получу одинаковые результаты; другими словами, отрицательное значение также является допустимым результатом. Итак, на самом деле есть два средних, пропорциональных данному уравнению:

Примечание: ваша книга (или преподаватель) может попросить вас рассматривать только положительное среднее пропорциональное, так как положительное значение находится между 3 и 12.Фактически, ваша книга (или преподаватель) может определять «среднее пропорциональное» как только и всегда положительное значение. Используйте определение, данное вашей книгой (или инструктором), но имейте в виду, что вы можете встретить другие определения в других классах или контекстах.

Найдите положительное среднее, пропорциональное 4 и 25.

Чтобы найти средства, я составлю уравнение и решу:

4/ x = x /25

4 × 25 = x ²

100 = x ²

± 10 = х

Поскольку они указали, что хотят получить положительное среднее значение, мой ответ:

Возможно, вы заметили, что в приведенных выше решениях я всегда получал квадрат значения, равный числу, а затем извлекал квадратный корень из каждой стороны уравнения.Это дает быстрый метод решения для среднего пропорционального:

Найдите среднее значение, пропорциональное от 8 до 50

Они указали, что им нужно значение, которое находится «между» двумя заданными значениями, и эти значения являются положительными, поэтому я знаю, что они хотят положительного решения. Вместо того, чтобы задавать пропорции, перемножать и решать квадратное уравнение, я сразу перейду к квадратному корню:

квадратных [8 × 50]

кв.м [400]

sqrt [16 и 25 раз]

4 и 5 раз = 20

И это окончательное значение — мой ответ:

(Кстати, хотя это очень необычно, вы можете увидеть упражнение, в котором крайние значения пропорции (то есть заданные значения в упражнении «найти среднее пропорциональное») являются отрицательными.Когда эти значения умножаются, знаки «минус» погаснут, и вы, как обычно, можете извлечь квадратный корень.

(Однако невозможно иметь пропорцию, в которой крайние значения имеют противоположные знаки. Почему? Потому что произведение крайних значений противоположных знаков будет отрицательным, и вы не можете извлечь квадратный корень из отрицательного числа. Если вас когда-либо просят найти среднее значение, пропорциональное двум значениям с противоположными знаками, имейте в виду, что это вопрос с подвохом!)

Найдите (положительное) среднее, пропорциональное
³/₂ и ³/₈

Тот факт, что во всех примерах, приведенных в учебнике, были целые числа, не означает, что пропорция не может содержать дроби; это может.Я использую сокращенный метод решения, умножая два крайних значения, а затем извлекая (положительный) квадратный корень:

(3/2) × (3/8) = 9/16

sqrt [9/16] = 3/4

Таким образом, среднее пропорциональное двух дробей является другой дробью:

Вы также можете услышать «среднее пропорциональное», называемое «геометрическим средним».Это потому, что эта пропорциональная зависимость возникает в геометрии прямоугольных треугольников. Если мы возьмем прямоугольный треугольник и проведем линию от прямого угла к гипотенузе так, чтобы эта линия была перпендикулярна гипотенузе, то гипотенуза будет разделена на две части. Перпендикулярную линию можно рассматривать как линию, указывающую высоту « h » треугольника, когда гипотенуза является основанием. Эти две части помечены « x » и « y » на рисунке ниже:

Можно доказать, что высота h и две части, x и y , образуют пропорцию:

В частности:

Эту взаимосвязь можно превратить в упражнения, например:

Учитывая треугольник ниже, с
x = 132 и y = 44, найдите высоту h треугольника.

Когда прямоугольный треугольник устроен таким образом, с линией высоты, проведенной от прямого угла к гипотенузе, высота и две части основания образуют пропорцию, в которой высота является средней пропорциональной двух частей. Итак, чтобы найти высоту, мне нужно найти среднее значение, пропорциональное двум значениям, которые они мне дали.

Тогда коэффициент I:

И затем извлекаю квадратный корень:

sqrt [(16) (121) (3)] = (4) (11) sqrt [3]

Затем, умножив это, я обнаружил, что высота треугольника составляет:

URL: https: // www.purplemath.com/modules/ratio3.htm

Пропорции — Объяснение и примеры

Трудно представить, какой была бы наша жизнь без математических понятий, таких как пропорции. В нашей повседневной жизни мы часто сталкиваемся с пропорциями и пропорциями, когда идем за покупками, готовим, во время профессиональной поездки и т. Д.

Соотношения и пропорции необходимы для — эффективной работы.В этой статье мы узнаем, как рассчитать пропорции и применить полученные знания для решения типовых задач, но перед этим давайте начнем с определения соотношений.

Коэффициент — это способ сравнения двух или более величин. Знак, используемый для обозначения отношения, — двоеточие «: » Предположим, что a и b — две разные величины или числа, тогда отношение a к b можно записать как a / b или a: b. Точно так же отношение b к a также может быть представлено как b: a или b / a. Первая величина в соотношении называется антецедентом, а вторая величина — как следствие.

Примеры соотношений: : или 3: 4, 1/5 или 1: 5, 199/389 или 199: 389 и т. Д. Из этого примера очевидно, что соотношение — это просто дробь, в которой антецедент равен числитель и консеквент являются знаменателем.

Знаменитый рисунок Витрувианского человека Леонардо да Винчи был основан на идеальных пропорциях человеческого тела. Каждая часть тела занимает разное соотношение, например, лицо занимает около 1/10 от общей высоты, а голова занимает около 1/8 от общей высоты.Писатели средневековья впервые использовали слово proportio (пропорция). В 1948 году Ле Корбюзье дал систему пропорций.

Что такое пропорция?

Пропорция — это выражение, которое говорит нам, что два отношения эквивалентны. Два отношения называются пропорциональными, если они эквивалентны. Пропорции обозначаются знаком «:» или «=». Например, если a, b, c и d — целые числа, тогда пропорция записывается как a: b = c: d или a / b = c / d или b: a = d: c.Например, отношения 3: 5 и 15: 25 пропорциональны и записываются как 3: 5 = 15: 25

Четыре числа a, b, c и d известны как члены пропорции. Первый a и последний член d называются крайними членами, а второй и третий члены в пропорциональном выражении называются средними членами.

Как решить пропорции?

Легко вычислить, пропорциональны ли соотношения. Чтобы проверить, пропорционально ли соотношение a: b и c: d.

Умножьте первый член на последний член: axd
Умножьте второй член на третий член: bxc
Если произведение крайних членов равно произведению средних членов, то отношения пропорциональны: axd = bxc

Непрерывная пропорция

Говорят, что два отношения a: b и b: c находятся в непрерывной пропорции, если a: b = b: c.В этом случае член c называется третьей пропорцией a и b, тогда как b называется средней пропорцией между членами a и c.

Когда члены a, b и c находятся в непрерывной пропорции, получается следующая формула:

a / b = b / c

Перекрестное умножение членов дает; a x c = b x b, Следовательно,

b² = ac

Пример 1

Выясните, пропорциональны ли следующие соотношения: 8:10 и 12:15.

Пояснение

Умножьте первый и четвертый члены отношений.

8 × 15 = 120

Теперь умножьте второй и третий член.

10 × 12 = 120

Поскольку произведение крайностей равно произведению средних,
Так как произведение средних (120) = произведение крайностей (120),
Следовательно, 8 : 10 и 12:15 пропорциональны.

Пример 2

Проверьте, пропорционально ли соотношение 6: 12 :: 12: 24.

Пояснение

Это случай непрерывной пропорции, поэтому примените формулу axc = bxb,
В этом случае a: b: c = 6: 12: 24, следовательно, a = 6, b = 12 и c = 24
Умножьте первое и третье слагаемые:

6 × 24 = 144

Квадрат средних членов:

(12) ² = 12 × 12 = 144

Следовательно, соотношение 6:12:24 пропорционально.

Пример 3

Если 12: 18 :: 20: стр.Найдите значение x, чтобы соотношения были пропорциональными?

Объяснение

Дано: 12: 18 :: 20: p

Приравняйте произведение крайностей к произведению средств;
⇒ 12 × p = 20 × 18
⇒ p = (20 × 18) / 12

Решить относительно p;
⇒ p = 30
Следовательно, значение p = 30

Пример 4

Найдите третье, пропорциональное 3 и 6.

Объяснение

Пусть третье пропорционально быть c.
Тогда b² = ac
6 x 6 = 3 xc

C = 36/3

= 12

Таким образом, третье, пропорциональное 3 и 6, равно 12

Пример 5

Вычислить среднее пропорциональное между 3 и 27

Пояснение

Пусть среднее пропорциональное между 3 и 27 будет m.
Применяя формулу b² = ac; ‘

Следовательно, mxm = 27 x 3 = 81

m ² = 81
⇒ m = √81
⇒ m = 9
Следовательно, среднее значение, пропорциональное между 3 и 27, равно 9

Пример 6

Учитывая отношения a: b = 4: 5 и b: c = 6: 7, определите соотношение a: b: c.

Пояснение

Так как b — общий член между двумя отношениями;
Умножьте каждый член в первом соотношении на значение b во втором соотношении;

a: b = 4: 5 = 24:30,

Также умножьте каждый член во втором соотношении на значение b в первом соотношении;

b: c = 6: 7 = 30: 35

Следовательно, соотношение a: b: c = 24:30:35

Золотое сечение

Самым большим применением пропорции является золотое сечение , который очень помог в анализе пропорций различных объектов и искусственных систем, таких как финансовые рынки.Считается, что эти две величины находятся в золотом сечении, если их отношение равно отношению их суммы к большей из двух величин, то есть (a + b) / a = a / b, где a> b> 0.

Это соотношение обозначается греческой буквой φ. Дальнейшее упрощение этого уравнения дает φ ² — φ — 1 = 0. И решая это с помощью квадратичной формулы, мы получаем φ = 1.6180339887…

Евклид и многие математики после него работали над золотым сечением и обнаружили его существование. в правильном пятиугольнике и золотом прямоугольнике.

Практические вопросы

1. Определите значение пропущенной буквы в каждой из следующих пропорций.

а. 6: 9 = h: 15

б. т: 7 = 12: 21

с. 4: у = 8: 14

д. d: 3 = 0,4: 0,5

д. 1/3 ∶ 1/4 = 1/9:

f. 9: k = 6: 10

г. 2: 7 = м: 42

ч. 30: 25 = 42: r

i. x: 1,5 = 6,3: 4,5

2. Учитывая первый, второй и четвертый члены в пропорции 9, 21 и 77 соответственно.Вычислите значение третьего члена.

3. Стоимость 4 кг риса 28 долларов. Найдите стоимость 20 кг риса.

4. Отношение длины цветника к ширине 3/2. Рассчитайте длину цветника, если ширина 36 м.

5. В церковном хоре должны быть сформированы группы из мужчин и женщин. Если каждая группа должна состоять из 6 женщин и 4 мужчин. Сколько мужчин нужно, если в церкви 102 женщины?

Ответы

а. 10

б. 4

с. 7

г. 2.4

e. 1/12

ф. 15

г. 12

ч. 35

и. 2.1

2. 33

3. $ 140

4. 54 м

5. 68

Предыдущий урок | Главная страница | Следующий урок

Что такое пропорции | Типы | Примеры

Пропорция объясняется в основном на основе соотношения и дробей. Дробь, представленная в виде a / b, в то время как соотношение a: b, тогда пропорция указывает, что два отношения равны.Здесь a и b — любые два целых числа. Соотношение и пропорция являются ключевыми основами для понимания различных концепций как в математике, так и в естествознании.

Пропорция находит применение при решении многих повседневных жизненных проблем, например, в бизнесе, при совершении транзакций или во время приготовления пищи и т. Д. Она устанавливает связь между двумя или более количествами и, таким образом, помогает в их сравнении.

Что такое пропорция?

Доля, как правило, определяется как часть, доля или количество, рассматриваемые в сравнительном отношении к целому.Определение пропорции гласит, что когда два отношения эквивалентны, они пропорциональны. Это уравнение или утверждение, используемое для обозначения равенства двух соотношений или дробей.

Пропорция — Определение

Пропорция — это математическое сравнение двух чисел. Согласно пропорции, если два набора заданных чисел увеличиваются или уменьшаются в одном и том же соотношении, то говорят, что эти отношения прямо пропорциональны друг другу. Пропорции обозначаются символом «::» или «=».

Пропорция — Пример

Два отношения считаются пропорциональными, когда два отношения равны. Например, время, затрачиваемое поездом на преодоление 50 км в час, равно времени, затраченному им на преодоление расстояния 250 км за 5 часов. Например, 50 км / час = 250 км / 5 часов.

Продолжение пропорций

Говорят, что любые три величины находятся в непрерывной пропорции, если соотношение между первой и второй равно отношению между второй и третьей.Точно так же четыре количества в непрерывной пропорции будут иметь соотношение между первым и вторым, равное отношению между третьим и четвертым.

Например, рассмотрим два отношения: a: b и c: d. Чтобы найти непрерывную пропорцию для двух заданных членов отношения, мы преобразуем их средние в один член / число. В общем, это будет НОК средних, и для данного отношения НОК b и c будет bc. Таким образом, умножив первое отношение на c, а второе отношение на b, получим

Первое соотношение- ca: bc
Второе отношение- bc: bd

Таким образом, непрерывную пропорцию для данных соотношений можно записать в виде ca: bc: bd.

Соотношения и пропорции

Коэффициент — это способ сравнения двух одинаковых величин с помощью деления. Формула отношения для двух чисел a и b задается как a: b или a / b. Умножение и деление каждого члена отношения на одно и то же число (отличное от нуля) не влияет на соотношение.

Когда два или более таких отношения равны, говорят, что они находятся в соотношении .

Четвертый, третий и средний пропорциональный

Если a: b = c: d, то:

d называется четвертой пропорциональной a, b, c.
c называется третьим, пропорциональным a и b.
Среднее значение, пропорциональное между a и b, равно √ (ab).

Советы и рекомендации по пропорции

a / b = c / d ⇒ ad = bc
a / b = c / d ⇒ b / a = d / c
a / b = c / d ⇒ a / c = b / d
a / b = c / d ⇒ (a + b) / b = (c + d) / d
a / b = c / d ⇒ (a — b / b = (c — d) / d
a / (b + c) = b / (c + a) = c / (a + b) и a + b + c ≠ 0, тогда a = b = c.
a / b = c / d ⇒ (a + b) / (a - b) = (c + d) / (c — d), которое известно как правило componendo -dividendo
Если оба числа a и b умножаются или делятся на одно и то же число в соотношении a: b, то полученное соотношение остается таким же, как исходное соотношение.

Формула пропорции с примерами

Формула пропорции — это уравнение, которое можно решить для получения сравнительных значений. Для решения задач пропорций мы используем концепцию, согласно которой пропорция — это два равных друг другу соотношения.Мы имеем в виду это в смысле равенства двух дробей.

Предположим, что у нас есть любые две величины (или две сущности), и мы должны найти соотношение этих двух, тогда формула для отношения определяется как a: b ⇒ a / b , где,

a и b могут быть любыми двумя величинами.
«а» называется первым членом или антецедентом .
«b» называется вторым членом или последующим .

Например, в соотношении 5: 9 представляется как 5/9, где 5 является антецедентом, а 9 — следствием. 5: 9 = 10:18 = 15:27

Формула пропорции

Теперь предположим, что два соотношения пропорционально a: b и c: d. Два термина «b» и «c» называются «средствами или средними терминами», тогда как термины «a» и «d» известны как «крайние или крайние термины».

a / b = c / d или a: b :: c: d. Например, давайте рассмотрим другой пример количества учеников в 2 классах, где соотношение количества девочек и мальчиков равно. Наше первое соотношение количества девочек и мальчиков составляет 2: 5, а другое — 4: 8, тогда соотношение может быть записано как: 2: 5 :: 4: 8 или 2/5 = 4/8. Здесь 2 и 8 — крайности, а 5 и 4 — средние.

В зависимости от типа отношения, в котором участвуют два или более количества, пропорции можно разделить на разные типы.Есть два типа пропорций.

Прямая пропорция
Обратная пропорция

Прямая пропорция

Этот тип описывает прямую связь между двумя величинами. Проще говоря, если одно количество увеличивается, другое количество также увеличивается, и наоборот. Например, если скорость автомобиля увеличивается, он преодолевает большее расстояние за фиксированный промежуток времени. В обозначениях прямая пропорция записывается как y ∝ x.

Обратная пропорция

Этот тип описывает косвенную связь между двумя величинами. Проще говоря, если одно количество увеличивается, другое количество уменьшается, и наоборот. В обозначениях обратная пропорция записывается как y ∝ 1 / x. Например, увеличение скорости автомобиля позволит преодолеть фиксированное расстояние за меньшее время.

Важные примечания

Пропорция — это математическое сравнение двух чисел.
Основные пропорции бывают двух типов: прямые пропорции и обратные пропорции.
Мы можем применить концепции пропорций к географии, сравнивая величины в физике, диетологии, кулинарии и т. Д.

Свойства пропорции

Пропорция устанавливает эквивалентное соотношение между двумя соотношениями. Свойства пропорции, которой следует это отношение:

Дополнение — Если a: b = c: d, то значение каждого отношения равно a + c: b + d
Subtrahendo — Если a: b = c: d, то значение каждого отношения равно a — c: b — d
Дивидендо — Если a: b = c: d, то a — b: b = c — d: d
Componendo — Если a: b = c: d, то a + b: b = c + d: d
Alternendo — Если a: b = c: d, то a: c = b: d
Invertendo — Если a: b = c: d, то b: a = d: c
Компонент и дивидендо — Если a: b = c: d, то a + b: a — b = c + d: c — d

Разница между соотношением и пропорциями

Соотношение и пропорция — тесно связанные понятия.Пропорция означает равное соотношение между двумя или более соотношениями. Чтобы понять концепцию соотношения и пропорции, просмотрите разницу между соотношением и пропорцией, указанную здесь.

S.No		Пропорция
1	Отношение используется для сравнения размера двух вещей с одной и той же единицей измерения.	Пропорция используется для выражения отношения двух соотношений.
2	Это выражается двоеточием (:) или косой чертой (/).	Это выражается двойным двоеточием (: 🙂 или равным символу (=)
3	Это выражение.	Это уравнение.
4	Ключевое слово для различения соотношения в проблеме — «к каждому».	Ключевое слово для различения пропорций в задаче — «вне».

Доля Связанные темы

Ниже приводится список тем, которые тесно связаны с Пропорцией в коммерческой математике. Эти темы также дадут вам представление о том, как такие концепции рассматриваются в Cuemath.

Часто задаваемые вопросы о пропорции

Что вы имеете в виду под коэффициентом?

Отношение — это математическое выражение, записанное в форме a: b, которое выражает часть формы a / b, где a и b — любые целые числа.Например, дробь 1/3 может быть выражена как 1: 3 в форме отношения.

Что такое пропорция в математике?

Как соотношение и пропорции используются в повседневной жизни?

Пропорции и пропорции используются ежедневно. Соотношения и пропорции используются в деловых операциях при работе с деньгами, сравнении количества по цене при совершении покупок и т.д. где говорится, что бизнес получает 2,50 доллара с каждой продажи.

Как узнать, составляют ли два соотношения пропорцию?

Если два отношения эквивалентны друг другу, то говорят, что они пропорциональны.Например, соотношения 1: 2, 2: 4 и 3: 6 являются эквивалентными соотношениями.

Как рассчитать пропорцию?

Пропорция рассчитывается по формуле пропорции, которая гласит: a: b :: c: d или a: b = c: d. Мы читаем это так, как «а» относится к «б», как «с» относится к «г».

Что такое разные типы пропорций?

Прямая пропорция — описывает прямую взаимосвязь между двумя величинами.Проще говоря, если одно количество увеличивается, другое количество также увеличивается, и наоборот.
Обратная пропорция — описывает косвенную связь между двумя величинами. Проще говоря, если одно количество увеличивается, другое количество уменьшается, и наоборот.

Каковы различные свойства пропорции?

Дополнение — Если a: b = c: d, то значение каждого отношения равно a + c: b + d
Subtrahendo — Если a: b = c: d, то значение каждого отношения равно a — c: b — d
Дивидендо — Если a: b = c: d, то a — b: b = c — d: d
Componendo — Если a: b = c: d, то a + b: b = c + d: d
Alternendo — Если a: b = c: d, то a: c = b: d
Invertendo — Если a: b = c: d, то b: a = d: c
Компонент и дивидендо — Если a: b = c: d, то a + b: a — b = c + d: c — d

Является ли 1/3 и 1/3 пропорциональным? (Формируют ли 1/3 и 1/3 пропорцию?)

Хотите узнать, составляют ли 1/3 и 1/3 пропорции? В этой статье мы сравним эти два значения, чтобы определить, существует ли пропорциональное соотношение между 1/3 и 1/3.Давайте приступим к делу!

Хорошо, в первую очередь мы говорим о пропорции, но ее также можно рассматривать как соотношение. Вопрос, который мы здесь действительно задаем, заключается в том, равно ли 1/3 1/3 в другой пропорции. Давайте посмотрим на это визуально и воспользуемся буквами, чтобы объяснить, как работают пропорции:

А / B знак равно C / D

Теперь они выглядят как дроби, и мы могли бы назвать верхнее число каждого числителем, а нижнее число каждого знаменателем, но при работе с пропорциями нам нужно относиться к ним по-разному.

Числа в позициях A и D называются «крайними значениями», а числа в позициях B и C называются «средствами».

Итак, как мы узнаем, пропорциональны ли 1/3 и 1/3 друг другу? Основное определяющее свойство любой пропорции состоит в том, что произведение средних значений равно произведению крайностей.

Что это значит? Проще говоря, это означает, что A, умноженное на D, должно равняться B, умноженному на C. Вы также можете рассматривать эти отношения как дроби, а затем упростить их до самых низких значений и сравнить их.Если они равны, то они пропорциональны.

Давайте сначала выясним, равно ли A (1) x D (3) B (3) x C (1):

1 х 3 = 3

3 х 1 = 3

Как мы видим, 3 действительно равно 3, поэтому мы можем сказать, что 1/3 и 1/3 ЯВЛЯЮТСЯ пропорциональными .

Давайте также попробуем это, уменьшив две доли / отношения до их наименьших значений и посмотрим, равно ли полученное соотношение.

1 / 3 знак равно 1/3

Уменьшая два отношения до их простейшей / наименьшей формы, мы можем увидеть, что простейшая форма 1/3 — это 1/3, а простейшая форма 1/3 — 1/3, поэтому 1/3 и 1/3 пропорциональны друг другу .

Вот и все, что нужно для сравнения 1/3 и 1/3, чтобы увидеть, пропорциональны ли отношения. Самый простой способ — убедиться, что произведение «средних» равно произведению «крайностей», путем умножения A и D, B и C, чтобы полученное число совпадало.

Надеюсь, это руководство помогло вам понять, как сравнивать дроби, и вы сможете использовать свои новые навыки, чтобы сравнивать, больше ли одна дробь другой или нет!

Цитируйте, ссылайтесь или ссылайтесь на эту страницу

Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большое одолжение и используйте инструмент ниже, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали.Мы очень ценим вашу поддержку!

Являются ли 1/3 и 1/3 пропорциональными?
«Пропорциональны ли 1/3 и 1/3?». VisualFractions.com . По состоянию на 17 августа 2021 г. https://visualfractions.com/calculator/proportion/is-1-3-and-1-3-proportional/.
«Пропорциональны ли 1/3 и 1/3?». VisualFractions.com , https: // visualfractions.ru / калькулятор / пропорция / is-1-3-и-1-3-пропорциональный /. По состоянию на 17 августа 2021 г.
Является ли 1/3 и 1/3 пропорциональным ?. VisualFractions.com. Получено с https://visualfractions.com/calculator/proportion/is-1-3-and-1-3-proportional/.

Случайный список примеров пропорций

Если вы зашли так далеко, вы должны ДЕЙСТВИТЕЛЬНО любить примеры пропорциональных соотношений. Вот несколько случайных вычислений для вас:

Соотношение и пропорции

Соотношение
Сравнение соотношений
Пропорция
Скорость
Скорость преобразования
Средняя скорость

Передаточное число

Коэффициент — это сравнение двух чисел.Обычно мы разделяем два числа в соотношении двоеточием (:). Предположим, мы хотим записать соотношение 8 и 12.
Мы можем записать это как 8:12 или как дробь 8/12, и мы скажем, что отношение восемь к двенадцати .

Примеры:

У Жаннин сумка с 3 видеокассетами, 4 шариками, 7 книгами и 1 апельсином.

1) Каково соотношение книг к шарикам?
В виде дроби с числителем, равным первой величине, и знаменателем, равным второму, ответ будет 7/4.
Два других способа записать соотношение: 7: 4 и 7: 4.

2) Каково соотношение видеокассет к общему количеству вещей в сумке?
Всего 3 видеокассеты и 3 + 4 + 7 + 1 = 15 штук.
Ответ может быть выражен как 3/15, от 3 до 15 или 3:15.

Коэффициенты сравнения

Чтобы сравнить коэффициенты, запишите их в виде дробей. Коэффициенты равны, если они равны, если записаны дробями.

Пример:

Равны ли отношения 3: 4 и 6: 8?
Коэффициенты равны, если 3/4 = 6/8.
Они равны, если их перекрестные произведения равны; то есть, если 3 × 8 = 4 × 6. Поскольку оба этих продукта равны 24, ответ — да, соотношения равны.

Не забывайте быть осторожными! Порядок имеет значение!
Соотношение 1: 7 не то же самое, что соотношение 7: 1.

Примеры:

Равны ли отношения 7: 1 и 4:81? Нет!
7/1> 1, но 4/81 <1, поэтому соотношения не могут быть равными.

Равны ли 7:14 и 36:72?
Обратите внимание, что 7/14 и 36/72 равны 1/2, поэтому два отношения равны.

Доля

Пропорция — это уравнение с соотношением сторон. Это утверждение, что два соотношения равны.
3/4 = 6/8 — это пример пропорции.

Если одно из четырех чисел в пропорции неизвестно, для нахождения неизвестного числа можно использовать перекрестные произведения. Это называется решением пропорции. Вместо неизвестного номера часто используются вопросительные знаки или буквы.

Пример:

Решите относительно n: 1/2 = n /4.
Используя кросс-произведение, мы видим, что 2 × n = 1 × 4 = 4, поэтому 2 × n = 4. Разделив обе стороны на 2, n = 4 ÷ 2, так что n = 2.

Оценка

Скорость — это коэффициент, который выражает, сколько времени нужно, чтобы что-то сделать, например преодолеть определенное расстояние. Пройти 3 километра за час — значит пройти со скоростью 3 км / ч. Дробь, выражающая скорость, имеет единицы расстояния в числителе и единицы времени в знаменателе.
Задачи, связанные с коэффициентами, обычно включают установку двух соотношений, равных друг другу, и решение для неизвестной величины, то есть решение пропорции.

Пример:

Хуан пробегает 4 км за 30 минут. С такой скоростью, как далеко он сможет пробежать за 45 минут?
Дайте неизвестному количеству имя n. В этом случае n — это количество км, которое Хуан мог пробежать за 45 минут с заданной скоростью. Мы знаем, что пробежать 4 км за 30 минут — это то же самое, что пробежать n км за 45 минут; то есть ставки такие же. Таким образом, у нас есть соотношение
4 км / 30 мин = n км / 45 мин, или 4/30 = n /45.
Находя перекрестные произведения и приравнивая их, мы получаем 30 × n = 4 × 45 или 30 × n = 180.Разделив обе стороны на 30, получим n = 180 ÷ 30 = 6, и ответ будет 6 км.

Коэффициенты пересчета

Мы сравниваем коэффициенты так же, как сравниваем коэффициенты, путем перекрестного умножения. При сравнении ставок всегда проверяйте, какие единицы измерения используются. Например, 3 километра в час сильно отличаются от трех метров в час!
3 километра / час = 3 километра / час × 1000 метров / 1 километр = 3000 метров / час
, потому что 1 километр равен 1000 метрам; мы «отменяем» километры при переводе в метры.

Важно:

Один из самых полезных советов при решении любой математической или научной задачи — всегда записывать единицы измерения при умножении, делении или преобразовании одной единицы в другую.

Пример:

Если Хуан пробегает 4 км за 30 минут, сколько часов ему потребуется, чтобы пробежать 1 км?
Будьте осторожны, чтобы не перепутать единицы измерения. Хотя скорость Хуана выражается в минутах, вопрос задается в часах. Только одна из этих единиц может использоваться при настройке пропорции.Чтобы преобразовать в часы, умножьте
на 4 км / 30 минут на 60 минут / 1 час = 8 км / 1 час
Теперь пусть на будет количеством часов, которое Хуану нужно, чтобы пробежать 1 км. Тогда пробег 8 км за 1 час будет таким же, как пробег 1 км за n часов. Решая пропорцию,
8 км / 1 час = 1 км / n часов, мы имеем 8 × n = 1, поэтому n = 1/8.

Средняя скорость

Средняя скорость поездки — это общее пройденное расстояние, разделенное на общее время поездки.

Пример:

Собака проходит 8 км со скоростью 4 км в час, затем гоняется за кроликом 2 км со скоростью 20 км в час. Какова средняя скорость собаки на пройденном расстоянии?
Общее пройденное расстояние составляет 8 + 2 = 10 км.
Теперь мы должны подсчитать общее время, в течение которого он путешествовал.
Первую часть пути он прошел 8 ÷ 4 = 2 часа. Он гнался за кроликом 2 ÷ 20 = 0,1 час. Общее время в пути 2 + 0,1 = 2,1 часа.
Средняя скорость его поездки 10/2.1 = 100/21 километр в час.

Соотношения и пропорции

MATH REVIEW: ПОЛЕЗНЫЕ МАТЕМАТИКИ ДЛЯ ВСЕХ

РАЗДЕЛ 1.2. СООТНОШЕНИЯ И ПРОПОРЦИИ

назад к Соотношения, стр. 1

A пропорция похоже на соотношение, за исключением того, что оно указывает на часть целого, и поэтому числитель возникает из знаменателя. Например, исследователь может говорят, что на каждые десять студентов в общежитии приходилось пять женщин.Пять на десять (5/10) — это пропорция. Пропорции должны иметь все числа в тех же единицах измерения и часто записываются в виде дробей.

Что происходит, когда вы хотите написать пропорцию, но числа даны в разных единицах? Предположим, вас попросили написать долю 3 чашки до 56 унций (3 чашки из 56 унций). Вы должны написать пропорцию из чашек в чашки (чашки: чашки) или из унций в унции (унции: унции), поэтому вам нужно будет преобразовать одно из чисел, чтобы оба числа были выражается в той же единице измерения.Переведем чашки в унции поэтому мы можем выразить соотношение как унции: унции. Поскольку есть 8 унций в одной чашке 3 чашки равны 24 унциям:

3 чашки * 8 унций / чашка = 24 унции

Сейчас два числа 3 чашки и 56 унций можно записать в следующем соотношении:

от 24 унций до 56 унций,
24:56,

или, теперь, когда единица измерения то же самое, 24:56 также можно записать как пропорцию:

24/56

Вы может потребоваться решить некоторые проблемы, связанные с соотношениями.

Если вы разделили 36 на две части в соотношении 1: 2 и одну часть это a, а другой — b, вы можете найти значение a и b:

Вы знаете, что

a + b = 36

a / b = 1/2

Вы можно использовать эти уравнения для решения относительно a и b, или вы можете использовать следующий простой метод:

Найти сколько единиц находится в 1 части отношения.Для этого разделите итог по количеству деталей.

Номер частей: 1 + 2 = 3.
Номер единиц в каждой части: 36/3 = 12.

Тогда, умножьте количество единиц в каждой части на количество частей в каждой переменной.

а = 1 * 12 = 12
б = 2 * 12 = 24

как в сторону.. .

В процентах настолько часто используются, что мы должны потратить на них немного времени здесь. Преимущество процентов заключается в том, что все они имеют тот же знаменатель: 100. Когда две дроби имеют одинаковый знаменатель, сравнения можно сделать очень легко.

0,21 = 21% = 21/100

в алгебраические выражения

Для подробнее об этом сайте свяжитесь с Distance Координатор по образованию.

Пропорции и соотношения — Бесплатная справка по математике

Определение коэффициента

Коэффициент — это отношение между двумя значениями. Например, соотношение 1 карандаша к 3 ручкам будет означать, что ручек в три раза больше, чем карандашей. Для каждого карандаша есть 3 ручки, и это выражается двумя способами, например: 1: 3 или дробью вроде 1/3.Не обязательно должно быть ровно 1 карандаш и 3 ручки, их должно быть несколько. С таким же успехом у нас могло бы быть 2 карандаша и 6 ручек, 10 карандашей и 30 ручек, или даже половину карандаша и полторы ручки! Фактически, именно так мы будем использовать отношения — чтобы представить отношения между двумя числами.

Определение пропорции

A пропорция банка использоваться для решения задач, связанных с отношениями. Если нам скажут, что соотношение колес к автомобилям составляет 4: 1, и что у нас в наличии на заводе 12 колес, как узнать количество автомобилей, которые мы можем оборудовать? Простая пропорция подойдет отлично.Мы знаем, что у нас соотношение 4: 1, а количество автомобилей, соответствующих этим 12 колесам, должно соответствовать соотношению 4: 1. Мы может настроить проблему следующим образом, где x — это наш недостающий номер Кол-во автомобилей:

Кому Чтобы решить такую пропорцию, мы будем использовать процедуру под названием перекрестное умножение . Этот процесс включает в себя умножение двух крайностей, а затем сравнение этот продукт с продуктом средств. Крайность — это первое число (4) и последнее число (x), а среднее значение — это 1 или 12.

Кому умножаем крайности, которые мы просто делаем \ (4 * x = 4x \). Продукт означает \ (1 * 12 = 12 \). Процесс очень прост, если вы помните это как перекрестное умножение, потому что вы умножаете по диагонали через знак равенства.

Вы затем следует взять два продукта, 12 и 4x, и надеть их противоположные стороны такого уравнения: \ (12 = 4x \). Решить относительно x разделив каждую сторону на 4, вы обнаружите, что \ (x = 3 \). Чтение возвращаясь к проблеме, мы помним, что x обозначает число машин с 12 шинами, и это наш ответ.2 \), что означает x равняется квадратному корню из 16, который равен 4 (или -4). Вы завершили этот урок, поэтому не стесняйтесь просматривать другие страницы этого сайта или ищите больше уроков по пропорциям.

Калькулятор соотношений и пропорций

Используйте инструмент ниже, чтобы преобразовать дроби в десятичные числа или взять заданное выражение отношения и найти неизвестное значение.

Как развести бензин для бензопилы: официальный сайт Echotool.

Почему нужно смешивать масло и бензин

Соотношение количества масла и бензина для топливной смеси

Пошаговая инструкция по заправке

Задачи на пропорции по математике — примеры с ответами

Понятие пропорции

Задачи на пропорции с решением и ответами

пропорция масла и бензина для бензопилы

Как варить рис рассыпчатым в кастрюле на воде

Универсальный рис длиннозерный

Что приготовить?

Как варить рис на воде

Нежный рис круглозерный

Что приготовить?

Как варить круглозерный рис на воде

Рассыпчатый рис обработанный паром

Что приготовить?

Как варить рис рассыпчатым в кастрюле

Практичный рис в пакетиках для варки

Как варить рис на гарнир

Хитрости опытных хозяек

Трюк с полотенцем

Капелька масла

Тонкий ореховый аромат

Желтый или белый

Готовим вместе с MAKFA

Просто о саженях и золотой пропорции — портфолио графического дизайнера Артёма Владимирова

Предисловие

§1. Начало. Ряд Фибоначчи

§2. Число Фи

§3. Золотое сечение

§4. Метрическая система

§5. Пропорции квадрата

§6. Интересные превращения числа Φ

§7. Система пропорций

§8. Образ, подобие, мера и каравай

§9. Золотая пропорция тела человека

§10. Казённая сажень отдельно

§11. Погрешность измерений

§12. Измерим себя и проверим

Калькулятор саженей

Другие статьи

Таблица пропорций и марок бетона на 1м3

Подходящие марки бетона

Заказать качественный бетон в компании «Бетонная индустрия»

Таблица «Пропорции бетона на 1м3». Качественные бетонные смеси

Технические характеристики бетона

Соответствие марки применению бетона

Основные компоненты бетонной смеси

Расход материалов. Таблица «Пропорции бетона на 1м3»

Пропорции состава бетона для фундамента

Порядок приготовления раствора

Проверка пропорциональности | Purplemath

Purplemath

MathHelp.com

Пропорционально ли

Является ли 42/55 пропорциональным 50/65? Обоснуйте свой ответ, не уменьшая дробей.

Пропорциональны ли 42/273 и 170/1105? Объясните свой ответ, не сокращая дроби и не переводя их в общий знаменатель.

Найдите среднее значение, пропорциональное 3 и 12.

Найдите положительное среднее, пропорциональное 4 и 25.

Найдите среднее значение, пропорциональное от 8 до 50

Найдите (положительное) среднее, пропорциональное

Учитывая треугольник ниже, с

Пропорции — Объяснение и примеры

Что такое пропорция?

Как решить пропорции?

Золотое сечение

Что такое пропорции | Типы | Примеры

Что такое пропорция?

Пропорция — Определение

Пропорция — Пример

Продолжение пропорций

Соотношения и пропорции

Четвертый, третий и средний пропорциональный

Формула пропорции с примерами

Формула пропорции

Прямая пропорция

Обратная пропорция

Свойства пропорции

Разница между соотношением и пропорциями