Расчет п образной лестницы
Результатами расчета станут:
- 3D модель поворотной лестницы на 180,
- подробные чертежи,
- рассчитанные размеры будущей лестницы с площадкой,
- существенная экономия вашего времени, которое вы бы потратили, рассчитывая все самостоятельно!
Данные для расчета лестницы с поворотом на 180 онлайн
Для онлайн расчета лестницы с поворотом на 180 градусов вам необходимо внести исходные данные — высоту проема (между чистым полом верхнего этажа и полом нижнего этажа), предполагаемую длину лестницы и ее ширину, а также предполагаемое количество ступеней (которое в процессе работы с калькулятором можно пробовать методом перебора для получения идеальной конструкции двухмаршевой лестницы).
Советуем выбирать нечетное количество ступенек для вашей деревянной лестницы — так будет удобнее по ней передвигаться, так как начинать и заканчивать движение будет одна и та же нога.
Рекомендации по идеальным размерам ступеней, оценке безопасности и комфортности лестницы будут приведены ниже.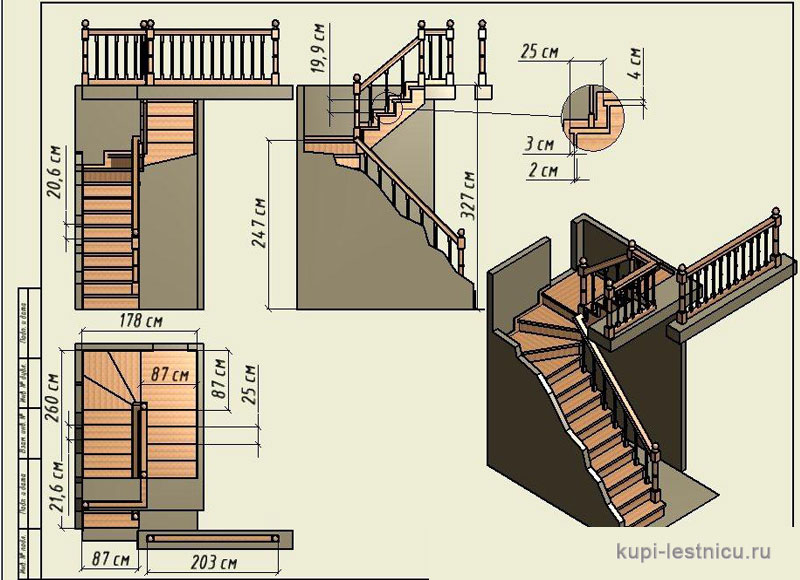
Какие данные вы получите в ходе расчетов?
Программа оценит введенные вами входные данные по свободному пространству в доме, которое вы хотите отвести под П — образную поворотную лестницу на 180 градусов. На основании введенных размеров будет рассчитан:
- угол наклона лестницы на косоурах, который вы самостоятельно сможете сравнить с приведенным ниже оптимальным углом.
- размеры ступеней и подступенков — высота, ширина
- размеры площадки
- размеры косоуров, размеры запилов
Также будут сформированы 3D модель лестницы и различные подробные чертежи.
Чертежи двухмаршевой лестницы с поворотом на 180 градусов
По итогам расчетов онлайн программа лестницы сформирует чертежи на соответствующих вкладках:
- вид лестницы сбоку
- вид лестницы сверху
- чертеж косоуров верхнего марша
- чертеж косоура нижнего марша
- подробный чертеж ступеней
Итоговые чертежи содержат все необходимые размерные обозначения.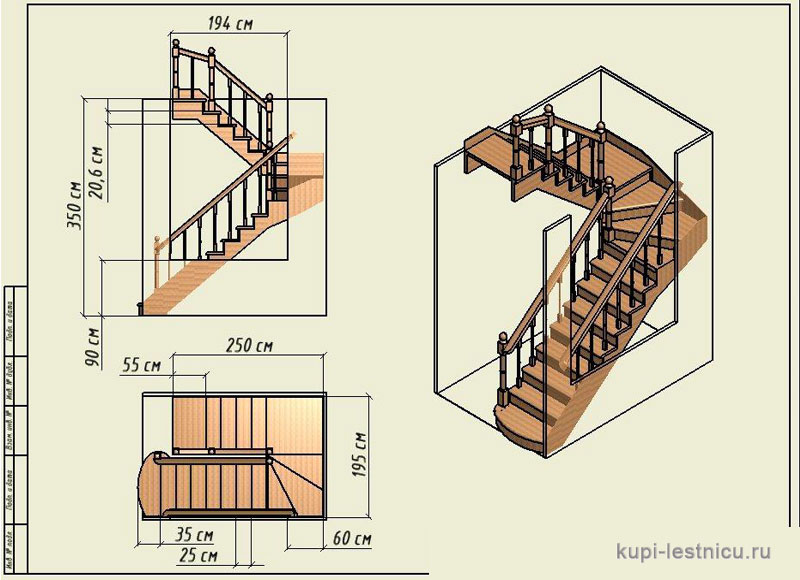
Давайте теперь посмотрим, какие же размеры и параметры присущи удобным, практичным и безопасным лестницам.
Оптимальные параметры лестницы для удобной конструкции
На стадии проектирования очень важно внимательно отнестись к требованиям высоты ступеней, углу наклона лестницы, ведь переделать в дальнейшем будущем уже построенную и неудобную лестницу будет очень сложно. На практике при проектировании и строительстве деревянной лестницы чаще всего используют следующие размерности и параметры:
- Угол наклона деревянной лестницы — 29 — 35 градусов. Всё, что ниже приближается по функциональности к пандусам, занимает много места в доме. Всё, что выше — приближается больше к чердачному варианту крутой приставной лестницы, ходьба по такой лестнице неудобна, зачастую просто опасна.
- Ширина лестницы. За стандартную величину в частном доме принимают 90 — 110 см. Если свободное пространство ограничено, можно ширину проема заузить, минимальное критическое значение — 80 см.
 Не забывайте, что по такой лестнице не только нужно будет ходить по одному человеку, но иногда переносить мебель и крупногабаритные предметы, которые попросту не поместятся в узкий проем.
Не забывайте, что по такой лестнице не только нужно будет ходить по одному человеку, но иногда переносить мебель и крупногабаритные предметы, которые попросту не поместятся в узкий проем. - Высота и ширина ступеней. Согласно стандартам максимальная удобная и нетравмоопасная высота ступенек не может превышать 200 мм. Обычно 15 — 17 см. Оптимальная ширина ступени 27 — 30 см — таким образом нога взрослого человека отлично помещается на ступень, а оптимальная высота ступени позволяет не напрягать сильно ноги во время подъема или спуска.
- Толщина ступени. Для изготовления ступеней используют деревянные доски толщиной 4 — 5 см (тонкая будет скрипеть). Для подступенка оптимальная толщина — 2,5 — 3 см.
- Свес ступени. Минимальный выступ деревянной ступени (свес) над подступенком — 30 мм, максимальный — 40 мм. Свес увеличивает поверхность ступени.
- Количество ступеней для одного пролета лестницы — не более 18 штук. В среднем 10 — 12, но, конечно, это зависит от длины марша.
 Советуем количество ступенек сделать нечетным — таким образом, начинать и заканчивать подъем или спуск по лестнице вы будете одной и той же ногой.
Советуем количество ступенек сделать нечетным — таким образом, начинать и заканчивать подъем или спуск по лестнице вы будете одной и той же ногой. - Высота перил должна начинаться от 90 см в целях безопасности.
- Высота в проходе лестницы — от любой ступеньки марша до пола верхнего этажа или перекрытия верхнего марша лестницы, должна составлять от двух метров.
- Толщина косоура — изготавливается из доски толщиной в среднем 5 — 7 см.
Если говорить о нагрузках, которые испытывает стандартная лестница в жилом доме — 300 кг/м². Прогиб не должен превышать 1/400 пролёта.
Расчет двухмаршевой лестницы с поворотом на 180 с помощью онлайн калькулятора KALK.PRO — удобный и простой способ рассчитать и спроектировать своими руками лестницу, благодаря корректным алгоритмам программы, наглядной 3D визуализации и подробным чертежам. Используйте калькулятор и сами убедитесь!
Эта статья будет полезна тем, кто хочет рассчитать лестницу с 1 на 2 этаж в таунхаусе и коттедже. Не важно, сами Вы будете изготавливать и устанавливать лестницу или заказывать в компании, но очень важно, чтобы Вы могли быть уверены, что это самая идеальная и удобная лестница.
Не важно, сами Вы будете изготавливать и устанавливать лестницу или заказывать в компании, но очень важно, чтобы Вы могли быть уверены, что это самая идеальная и удобная лестница.
В конце статьи Вы узнаете какое количество ступеней Вам нужно, какие размеры у ступеней будут, какая будет Высота каждой ступени, межэтажная площадка у вас будет или забежные ступени. Этот расчет будет являться техническим заданием по лестнице.
Я тот человек, который за 2017 год установил 410 лестниц. Конечно, я не делаю все своими руками и у меня есть своя команда. Но, думаю, что факта изготовления и установки 410 лестниц достаточно, чтобы Вы смогли дочитать эту статью до конца.
Почему я решил сделать эту статью? Когда я только начал заниматься лестницами на металлическом каркасе, я весь интернет перерыл в поисках полезного контента по расчету лестниц, но его чертовски мало. А тот, что полезен, имеет существенный минус в том, что он сложнодоступный для обычного человека и понятен только для строителя.
Конечно, есть очень много технических нюансов в каждом виде лестниц, но они не влияют на расчет лестницы.
Для того, чтобы мы с Вами разговаривали на одном языке и об одном и том же, посмотрите фотографии тех лестниц, которые можно рассчитать после прочтения данной статьи.
А теперь, чтобы укрепить Ваше понимание, что этот расчет подходит для Вашего дома или дачи, посмотрите фото домов, куда можно устанавливать такие лестницы.
Забегу вперед и скажу, что не каждый после прочтения статьи сможет провести расчет каркаса лестницы.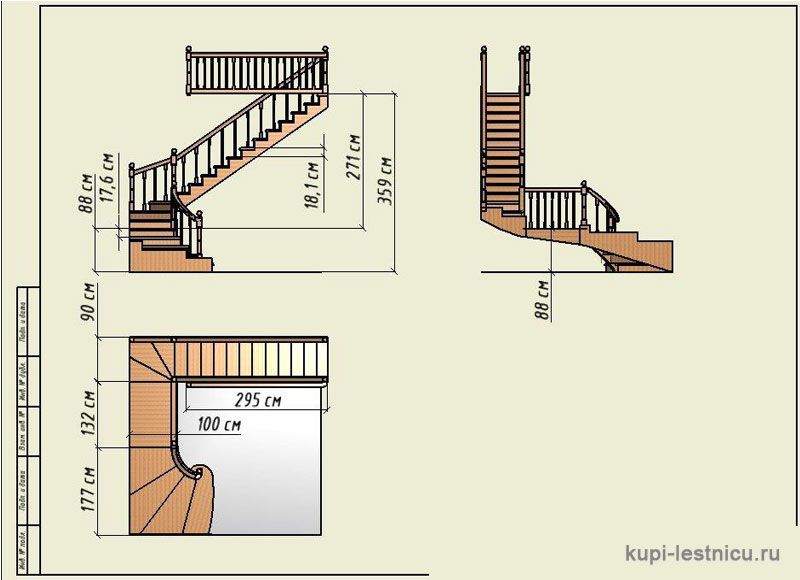 Если Вы уже подозреваете, что я говорю сейчас про Вас, то не переживайте, у меня для вас будет хорошая новость: если Вы сможете рассчитать себе лестницу, но у Вас останутся сомнения в правильности расчета, я с удовольствием проверю Ваш расчет и внесу правки. В конце статьи я расскажу подробнее об этом.
Если Вы уже подозреваете, что я говорю сейчас про Вас, то не переживайте, у меня для вас будет хорошая новость: если Вы сможете рассчитать себе лестницу, но у Вас останутся сомнения в правильности расчета, я с удовольствием проверю Ваш расчет и внесу правки. В конце статьи я расскажу подробнее об этом.
Мы будем делать расчет на П-образной лестнице, если у вас Г-образная, то не вешайте нос. Действия одинаковые.
Чтобы проще было понимать расчет лестницы, мы возьмем 1 конкретный объект, где будет стандартная П-образная лестница.
✔ Расчет высоты каркаса лестницы
Нам нужна высота от пола первого этажа до пола второго этажа.
Обратите внимание, что размер не от пола первого этажа до потолка, а именно от пола до пола. Очень важно чтобы этот размер был от чистого пола 1 этажа и чистового пола 2 этажа, если у Вас идет период строительства и стяжка еще не залита или стяжка есть, но нет еще напольного покрытия, то прикиньте приблизительно, на сколько миллиметров у Вас поднимется пол.
Очень важно чтобы размер был от чистого пола 1 этажа и чистового пола 2 этажа!
✔ Оптимальная длина металлической лестницы на второй этаж
Используйте для рассчета минимальный размер от стены, где будет поворот лестницы, до края торца перекрытия.✔ Расчет ширины металлического каркаса лестницы
Нам нужен размер от левой стены до правой стены.
Замерьте этот размер около торца перекрытия и около стены, которая идет параллельно перекрытию. Если размеры не сходятся берите из них минимальный размер.
*на фото представлена Г-образная шахта
Мы получили 3 размера
Зафиксируйте в таком формате свои размерыЧуть позже, я напишу, почему именно в таком формате необходимо зафиксировать эти размеры. Перед тем как погрузиться в детали расчета металлической лестницы на второй этаж, я вкратце расскажу Вам о том, что мы будем делать:
Четыре основных действия при расчете каркаса лестницы
- Рассчитываем приблизительное количество ступеней.
 Простая арифметика.
Простая арифметика. Подгоняем межэтажную площадку
☆ Если площадка не подойдет, то рассчитываем забежные ступени
и подгоняем количество ступеней на маршах лестниц
Производим более точный расчет количества ступеней, но не окончательный
Делаем окончальный расчет лестницы.
Сложно?
Сейчас поясню расчет металлического каркаса лестницы на образном примере:
Представьте себе дорогу на автомобиле от Москвы до Санкт-Петербурга.
Так же и с лестницей, мы не знаем, какая в конечном итоге получится лестница, но мы двигаемся от самого простого расчета лестницы к сложному.
Итак, едем дальше!
➤Первый шаг
Нам нужно понять примерное количество ступеней на Вашу лестницу.
Для этого нам нужно Вашу высоту разделить на стандартные высоты ступеней
и далее я этот параметр лестницы буду называть подступенком.
В нашем случаев высота составила 2800 мм.
Вот мой расчет
Формула: Высота/подступенок=количество ступеней
Это действие нам нужно повторить 5 раз.Делаем!2800/150=18,62800/160=17,52800/170=16,42800/180=15,52800/190=14,7Перед тем как делать выводы, я прокомментирую чтобы Вы не запутались:
Мы берем высоту от пола 1 этажа до пола 2 этажа
2800 делим на 5 стандартных размеров подступенка.
Результатом вычисления будет примерное количество ступеней.
Чтобы Вы сейчас не утонули в сомнениях, что стандартный подступенок 150 мм, а я рассматриваю вариант априори неудобной лестницы, я сразу скажу, что все верно. Всё дело в том, что по стандарту шаговая часть (проступь) 300 мм, а высота подступенка 150 мм, но на деле такое возможно в очень редких случаях. Это связано с тем, что для таких размеров нужно в 1.5 раза больше пространства для лестницы, чем обычно закладывают в малоэтажном строительстве. Другими словами, чтобы такую удобную лестницу сделать, у Вас должен быть проем для лестницы как в подъезде.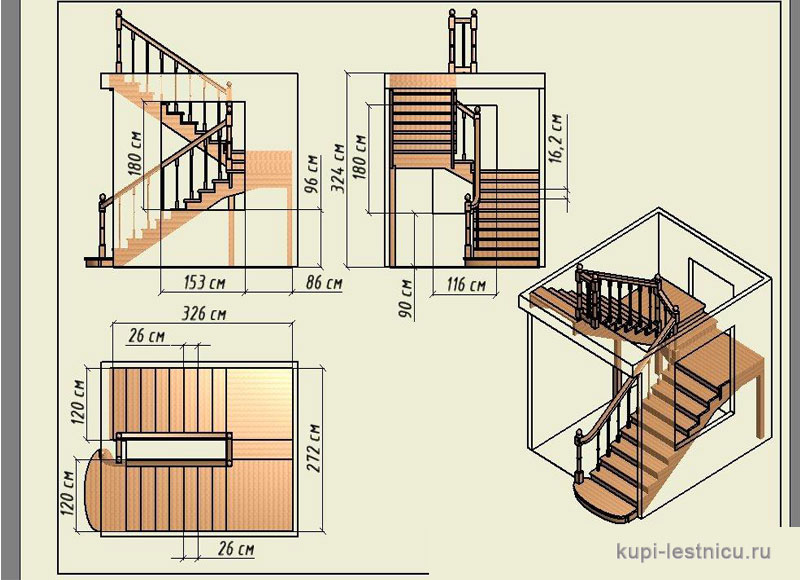
Когда заказчик строит частный дом, чаще всего он вообще не думает о лестнице и, когда я прихожу к нему на объект, он хватается за голову от удивления, какая у него неудобная лестница будет и что нужно, чтобы сделать хоть мало-мальски удобный вариант.
Или возьмем другой пример, таунхаусы в коттеджных поселках, где на этапе проектирования уже закладываются проемы под лестницу, но, при этом, никогда не получается проступь 300 мм и подступенок 150 мм. Чаще всего шаговая часть 250 мм и подступенок 170-180 мм. И, к слову сказать, это вполне удобные лестницы. Но! Если же застройщики будут делать таунхаусы так, чтобы входили стандартные лестницы,
то для Вас, как для заказчиков, цена дома будет на 10-15% дороже от застройщика.
Не привязывайтесь к размерам 300 мм и 150 мм, основывая на советах из интернета. Прочитайте статью до конца и Вы сможете сделать удобную лестницу!Подведем итоги расчета каркаса лестницы:
Мы берем результаты вычислений от минимального размера до максимального.
от 14.7 до 18,6 — это примерное количество ступеней, которое нам нужно уместить в проем лестницы, чтобы она была в пределах указанных параметров для удобного подъема и тем более спуска с лестницы.Но! мы не можем сделать 14 целых и семь десятых ступени или 18 целых и 6 десятых ступени, поэтому эти показатели количества ступеней нужно округлить:
✓ Большое число 18,6 округляем в большую сторону = 19 ступеней
✓ Меньшее число 14.7 округляем в меньшую = 14 ступеней
Для того, чтобы получилась комфортная лестница, мы должны разместить от 14 до 19 ступеней.➤Второй шаг
Зная примерное количество ступеней, мы можем перейти к ориентировочному размещению элементов лестницы. Нам нужно разместить элементы лестницы таким образом, чтобы попасть в диапазон от 14 до 19 ступеней.
Для того, чтобы научиться размещать элементы лестницы, нужно понимать какими вообще бывают.
✔ Прямые элементы (марши)
✔ Поворотные элементы
Обратите внимание на порядок размещения этих элементов.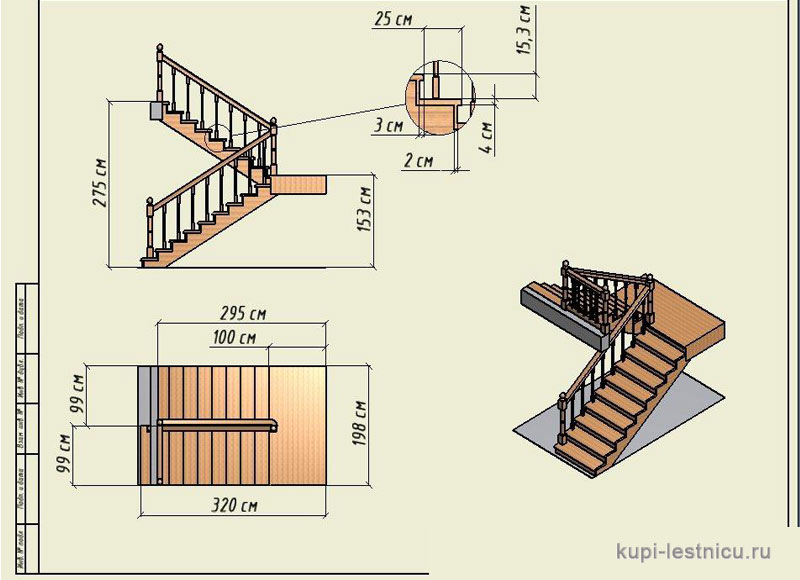 Когда мы будем подгонять эти элементы, то мы сначала будем идти от самого просто (1) к самому сложному (5). Другими словами, если 1й элемент не подходит, мы подставляем 2й элемент, если он не подходит, то 3й элемент и тд.
Когда мы будем подгонять эти элементы, то мы сначала будем идти от самого просто (1) к самому сложному (5). Другими словами, если 1й элемент не подходит, мы подставляем 2й элемент, если он не подходит, то 3й элемент и тд.
Видео удалено.
| Видео (кликните для воспроизведения). |
Как мы узнаем подходит ли элемент или нет? Это станет понятно, когда мы дойдём до конца расчета металлической лестницы на второй этаж.
Для того, чтобы получить идеальную лестницу, мы эти элементы лестницы будем подгонять: добавлять ступени, убирать ступени, делать их шире, делать их уже. Вместо межэтажной площадки пробовать другие элементы лестниц по убыванию удобства элемента, делать их шире и делать их уже.
Далее следуют арифметические вычисления, мужайтесь!
Размещение элементов лестницы начинается с поворотных элементов. Для начала берем межэтажную площадку.
У нас межэтажная площадка с размерами 2000 мм на 1000 м.
Изначальные размеры зависят от Вашего проема. Так как у нас ширина проема 2000 мм, то и ширина площадки тоже 2000 мм. Если бы ширина проема была 1800 мм, то и ширина площадки была 1800 мм.
У нас есть 2000 мм (2 м), чтобы разместить туда марш лестницы.
Значит и длина марша будет 2000мм (2м).
Мы берем расстояние 2000 мм (2 м) делим на популярную шаговую часть ступени 250 мм).
Отвечу заранее на вопрос почему мы берем 250 мм (25 см) шаговую часть, потому что это самая популярная шаговая часть ступени и с нее проще делать расчеты, потому что она делится равными частями на 1000 мм (1м).
Самая удобная и поэтому самая популярная шаговая часть ступени 250 мм (25см)
2000 (длина шахты)/250 (шаговая часть)=8 ступеней
Так как у нас ширина шахты с обеих сторон по 3000 мм, мы размещаем одинаковые марши с обеих сторон. Получается такая картина:
➤Третий шаг
Теперь предварительно проверим показатели лестницы:
Посчитаем какое количество ступеней у нас получилось. Получилось 17 ступеней, 16 прямых и 1 поворотная (межэтажная площадка тоже считается ступенькой, как и все остальные поворотные фрагменты). Теперь рассчитаем подступенок.
Получилось 17 ступеней, 16 прямых и 1 поворотная (межэтажная площадка тоже считается ступенькой, как и все остальные поворотные фрагменты). Теперь рассчитаем подступенок.
В нашем примере: 2800/17=164,7 мм
164,7 мм- это высота подступенка. Это 164 миллиметра и семь десятых миллиметра. Естественно, эту цифру нужно округлить (даже линейка, которая продается в магазине, с делениями по миллиметрам имеет свою погрешность, как и всё в мире)
Невозможно будет сделать лестницу с подступенком 164, 7. Так как обычные станки и балгарки не режут металл или дерево с такой погрешностью.
А, так как, мы не строим космический корабль, который полетит на Марс, а всего лишь лестницу, то мы округляем этот параметр до миллиметра.
Резюме: высоту подступенка округляем до 165 мм
Подытожим все параметры, по которым мы будем сравнивать удобство лестницы.
У Вас может возникнуть вопрос: «Куда уйдет погрешность в 0. 3 мм, если мы округлили цифры 164,7 до 165?» Ответ: отклонение уйдет на нижнюю ступень, она будет отличаться от всех остальных. 17 * 0.3 мм = 5.1 мм.
3 мм, если мы округлили цифры 164,7 до 165?» Ответ: отклонение уйдет на нижнюю ступень, она будет отличаться от всех остальных. 17 * 0.3 мм = 5.1 мм.
Это значит что первая ступень у нас будет на 5.1 мм короче чем остальные.
Если вы дошли до этого момента и все поняли- это очень круто!
Поздравляю, Вы сейчас впервые рассчитали лестницу!
Все же, если для Вас это темный лес, ничего страшного, дочитайте статью до конца, там будет расчет по Вашим размерам. Но не перелистывайте сразу вниз, Вам хотя бы немного нужно уловить логику расчета.
➤Четвертый шаг
У нас получилась вполне комфортная конструкция.
Итак, мы имеем 17 ступеней. 16 прямых и одну межэтажную площадку.
Высота подступенка 165 мм, проступь 250 мм.
Но! Тут еще есть один показатель- это 17 подъемов, давайте разберем его подробнее, я расскажу, чем он отличается от кол-ва ступеней.
Этот показатель отличается от количества ступеней на 1 единицу (прибавить +1 к количеству ступеней, не более).
Это зависит от следующего: используется ли пол второго этажа в качестве ступени или не используется.
Мы просто делаем так, что верхняя ступень лестницы будет являться полом второго этажа (правый вариант на фото выше). Поэтому может получиться так, что у нас 17 ступеней и 18 подъемов. Этот дополнительный подъем мы будем отображать вот таким хвостиком со стороны верхней ступени
Теперь для выбора у нас есть два варианта лестницы:
Другие варианты в данном случае мы не будем рассматривать и из этих вариантов будем выбирать какую лестницу делать.
Конечно, самый удобный вариант- это второй, так как получилась практически идеальная высота подступенка и стандартная шаговая часть.
Первый вариант лестницы нужно будет ставить только в случае каких-то технических нюансов на объекте. К примеру, возникла необходимость удлинить перекрытие и сделать так, чтобы каркас занимал меньше пространства или на той стене, к которой прилегает площадка, расположено окно (радиатор обогревательный, электрический щиток). В этом случае придется пожертвовать немного комфортом, поднимая межэтажную площадку, отказываясь от дополнительного подъема, за счет того, что сделали бы пол второго этажа последней ступенью.Вот теперь Вы точно и окончательно посчитали лестницу!
К примеру, возникла необходимость удлинить перекрытие и сделать так, чтобы каркас занимал меньше пространства или на той стене, к которой прилегает площадка, расположено окно (радиатор обогревательный, электрический щиток). В этом случае придется пожертвовать немного комфортом, поднимая межэтажную площадку, отказываясь от дополнительного подъема, за счет того, что сделали бы пол второго этажа последней ступенью.Вот теперь Вы точно и окончательно посчитали лестницу!
Получилось? Давайте проверять!
Как проверить правильность своего расчета металлического каркаса лестницы:Берите карандаш, и прямо на стене начиная снизу отрисовывайте габариты ступени. Таким образом, Вы сможете немного «пощупать» как будет выглядеть лестница, будет ли она удобна. И если на том месте где будет лестница есть технические нюансы (электрический щиток, трубы, окно, дверь), Вы сможете проверить не будет ли косяка и не нужно ли будет переделывать лестницу из-за этого нюанса.
Или скидывайте информацию мне (обязательно в том формате, в котором я рисовал для нашего расчета) и я Вам обязательно помогу.
Так же в данном расчете не предусмотрено наличие ступеней за проемом под лестницу, но такое часто может быть
Если Вы карандашиком сами нарисуете на стене будущую лестницу, то Вы сможете увидеть, сколько еще ступеней можно добавить к лестнице.
➤БОНУС
Если Вы дочитали эту статью до конца, Вам нужна моя помощь и перепроверка Ваших расчетов, то присылайте свои данные на мою почту [email protected] и примерный расчет, если он есть.
Маленькая просьба) Присылайте именно в таком формате, чтобы была уверенность что мы друг друга понимаем.
✔ Размеры присылайте в таком формате
✔Свой расчет в таком формате:
Я постарался Вам передать базу знаний. Она должна закрыть большинство сложностей с расчетом лестницы. Но, так как каждая лестница индивидуальна, скидывайте Ваш расчет лестницы на проверку и я Вам обязательно отвечу.
Посмотрите видеоурок к этой статье по расчету лестницы:
Делайте правильную и удобную лестницу, помните, что она должна прослужить Вам долгие годы!Кстати, посмотрите видеообзор дизайнерской лестницы в таунхаусе и на практике узнайте, как использовать расчет лестницы.
П-образная лестница является достаточно удобной и практичной из-за наличия поворотной площадки П-образная лестница имеет поворотную площадку на 180 градусов. Такая конструкция достаточно удобная для людей любого возраста и занимает мало места в помещении. Чтобы подъем был удобен, необходимо делать угол наклона лестницы от 30ᵒ до 40ᵒ, тогда можно будет безопасно подниматься, как пожилым людям, так и маленьким деткам.
Материалы для П-образных лестниц на второй этаж дома
Конструкция лестницы изготавливается из любого доступного материала.
Для изготовления лестницы для загородного дома лучше использовать ценную породу древесины
А именно:
- Из дерева крепких пород – зачастую, для подобных целей, чаще всего, используется дуб. Подобный материал удобен тем, что он легко обрабатывается, и имеется в достаточном количестве в любом строительном супермаркете.
- Из металла – очень красиво и дорого смотрится ковка, сделанная профессионалом.
 Она не только будет придавать комнате завершенный вид, и облагораживать помещение, но и прослужит не один десяток лет.
Она не только будет придавать комнате завершенный вид, и облагораживать помещение, но и прослужит не один десяток лет. - Бетонные лестницы являются наименее затратными, но они не создают ощущения уюта и теплоты, а лишь ассоциацию с подъездной площадкой.
- Плитка и ламинат используются довольно редко, ведь главным правилом создания лестниц является гармония с окружающим пространством, а при применении подобного материала, конструкция может сливаться с полом, и создавать дисгармонию.
Также можно применять комбинацию двух или нескольких материалов между собой. Это позволит создать интересное и оригинальное творение, подчеркивающее стиль помещения и быть достаточно удобным.
Виды П-образных лестниц с площадкой и без
Существует 2 вида лестниц, имеющих П-образную форму.
А именно:
- С наличием забежных поворотных ступеней – при подобной планировке вместо площадки прикрепляются несколько дополнительных ступенек, они создают небольшой виток и позволяют перестроиться человеку на продолжение подъема.
 Подобные чертежи и созданная по ним лестница будет менее удобной для пожилых людей и детей, поэтому необходимо учитывать этот фактор, разрабатывая ее размеры в режиме онлайн, а затем воплощая их в жизнь. Ширина ступеней в подобной конструкции должна быть в наиболее узком месте – от 10 см, а в самой широкой – более 25 см. Если изготовление лестницы происходит своими руками, то могут возникнуть проблемы во время правильной нарезки ступеней, поэтому перед началом работы, лучше проконсультироваться со специалистом, чтобы не испортить дорогостоящий материал.
Подобные чертежи и созданная по ним лестница будет менее удобной для пожилых людей и детей, поэтому необходимо учитывать этот фактор, разрабатывая ее размеры в режиме онлайн, а затем воплощая их в жизнь. Ширина ступеней в подобной конструкции должна быть в наиболее узком месте – от 10 см, а в самой широкой – более 25 см. Если изготовление лестницы происходит своими руками, то могут возникнуть проблемы во время правильной нарезки ступеней, поэтому перед началом работы, лучше проконсультироваться со специалистом, чтобы не испортить дорогостоящий материал. - С наличием площадки – подобные конструкции чаще всего встречаются в домах, и объясняется подобный расчет тем, что они являются наиболее комфортными для всех членов семьи, независимо от возраста. Единственным минусом их в частном доме является то, что они занимают достаточное количество свободного места, и, соответственно, на их сооружение потребуется больший расход стройматериалов.
Существуют П-образные лестницы как с площадкой, так и без, поэтому только вам решать какую выбирать
Какую выбрать П-образную лестницу, с наличием площадки или без нее, решать только владельцу.
Но, делая подобный выбор, нужно учитывать и определенные факторы – наличие достаточного количества денежных средств не только на покупку стройматериалов, но и на оплату работникам при установке, количество членов семьи, проживающих в доме и их средняя весовая категория.
[1]
Если в доме есть инвалиды или люди с определенными проблемами со здоровьем, это также нужно учитывать, ведь не всегда можно вовремя прийти им на помощь.
Правила безопасности для лестниц на 180 градусов
Наиболее правильным вариантом является заказ лестницы в специализированной фирме.
Профессионал приедет на место, и сделает необходимые замеры, создаст чертеж на компьютере и подкорректирует его под требования хозяев.
[2]
Чтобы не натолкнуться на недобросовестного производителя, и получить в результате привлекательную и удобную конструкцию, необходимо придерживаться ряда правил.
Для того чтобы П-образная лестница была безопасной и надежной, лучше обратиться за помощью к специалистам
А именно:
- Лестницу на 180 градусов делают в наиболее редких случаях, если действительно не хватает места на более объемную и безопасную конструкцию, чтобы по ней можно было быстро передвигаться.

- Отдавать предпочтение известной фирме, имеющей много хороших отзывов.
- Перед тем, как взять предварительный платеж, фирма должна приехать на место и сделать предварительные замеры, и создать онлайн-проект лестницы. Если подобную работу накладывают на владельца, лучше отказаться от их услуг, ведь даже малейшая ошибка в замере может понести за собой много нюансов, и человек получит в результате финансовый ущерб и неудобную или неправильно сделанную конструкцию.
- После установки, необходимо обязательно протестировать лестницу – пройдясь по ней, пробежав по ней, и чтобы не было слышно скрипа, пошатывания, или узких ступенек.
При любых неполадках, нужно обязательно требовать их устранения на месте, чтобы в дальнейшем это не привело к трагическим последствиям.
Советы по онлайн-расчету П-образной лестницы от специалистов
Чтобы произвести правильный расчет схемы и материалов для лестницы частного дома, необходимо соблюдение нескольких правил.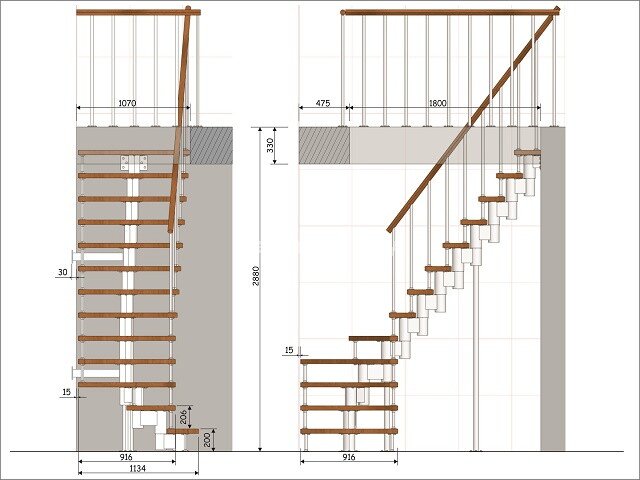
Перед изготовлением и установкой П-образной лестницы, следует правильно произвести расчеты как конструкции, так и помещения
А именно:
- Просчитывать размеры, необходимо опираясь на параметры среднестатистического человека. Существует 3 формулы – безопасности, удобства и шага. Каждая является важным соло в формуле, поэтому пренебрегать ими не стоит. Готовая конструкция, сделанная по правилам, будет не только радовать глаз хозяев, но и удобной, комфортной не только для ходьбы, но и переноски вещей.
- Высота перил должна составлять не менее 90-95 см, а количество балясин должно совпадать с количеством ступеней или более, расстояние – не более 55 см.
- Наиболее комфортной шириной марша является 90 см.
- Чтобы не доставлять дискомфорта высоким людям, высота от ступеней до потолка должна быть не менее 2 м.
- Перила должны быть изготовлены из материала, который бы не доставлял дискомфорта во время подъема – древесина должна быть идеально отполирована, зашлифована и покрыта лаком или краской, металл лучше покрыть специальными накладками, чтобы в зимнее время рукам не было холодно, ведь особенно неприятно это для пожилых людей и детей.

- На ступени лучше положить специальные ковровые покрытия, с наличием клейкой внутренней стороны или крепежа. Это позволит снимать их для уборки и быть безопасными во время бега или передвижения.
- Цветовая гамма лестницы, ковриков и общего стиля комнаты должны совпадать и гармонично сочетаться между собой, тогда у вошедшего в комнату человека не будет создаваться впечатления незавершенности или перебора в дизайне.
- Красиво смотрятся кованые балясины, на выбор дизайнера, они могут быть, как покрашены однотонной краской, так и добавлены некоторые мазки бронзой, позолотой или легкие переливы серебра.
- Древесина также не будет скучной, если в арсенале дизайнера или хозяина присутствует фантазия и желание преобразить лестничную конструкцию – множество резных элементов способны превратить обычную балясину в произведение искусства. Это будет гармонично смотреться в стиле барокко, и незаменимо в классическом интерьере.
Подчеркнут дороговизну и шик творения красные ковровые накладки, превращающие обычную лестницу в ковровую дорожку. Единственным минусом этого творения является его стоимость – зачатую, она обходится довольно дорого, ведь, в основном, применяется ручная работа, что является залогом ценности и оригинальности.
Единственным минусом этого творения является его стоимость – зачатую, она обходится довольно дорого, ведь, в основном, применяется ручная работа, что является залогом ценности и оригинальности.
П-образные лестницы (видео)
Следуя подобным советам, можно не огорчиться в полученном результате, а наслаждаться комнатой долгое время.
Дизайн П-образной лестницы (фото интерьера)
Самой распространённой лестницей является П-образная, это хорошо знакомая нам железобетонная лестница, она установлена во всех многоэтажках массовой застройки, поднявшись по пролёту на половину этажа, нужно повернуться на 180 градусов, и продолжить движение на этаж. Для поворота предусмотрены прямоугольная площадка.Лестничные пролёты изготавливаются по СНиПам, для индивидуального строительства возникает необходимость произвести расчет п-образной лестницы, так как высота этажей может быть различной, как и размеры помещения, в котором надо построить лестницу.
Сначала надо собрать исходные данные, произвести замеры помещений, которые будет соединять лестница, сделать эскиз. На месте надо внимательно замерить все выступающие части, будь-то окна, трубы отопления, батареи. По эскизу сразу определяется ширина свободного пространства — проёма для установки лестницы. Ширина лестницы (длина ступени) будет составлять половину этого проёма, за вычетом небольших конструкционных деталей. Строители стараются ширину лестницы выполнять равной 1 метр.
На месте надо внимательно замерить все выступающие части, будь-то окна, трубы отопления, батареи. По эскизу сразу определяется ширина свободного пространства — проёма для установки лестницы. Ширина лестницы (длина ступени) будет составлять половину этого проёма, за вычетом небольших конструкционных деталей. Строители стараются ширину лестницы выполнять равной 1 метр.
П-образная конструкция предполагает устройство площадок поворота, чаще всего устраивают прямоугольные площадки. Если ширина площадки — это известная ширина проёма, то минимальная глубина площадки соответствует длине ступени. Оптимальной глубиной площадки является двойная длина ступени, для длины ступени 1 метр, глубина площадки составит 2 метра.
Осталось сделать самое главное, рассчитать параметры ступени. Для чего нужно измерить расстояние от пола до уровня пол следующего этажа. Фактически это высота потолка и ширина перекрытия. Пусть высота потолка будет 3000 мм, при толщине перекрытия 200 мм, следовательно высоту 3200 мм надо преодолеть двумя лестничными маршами. Легко определить, что каждый марш поднимет человека на 1600 мм.
Легко определить, что каждый марш поднимет человека на 1600 мм.
Принимая высоту ступени 160 мм, получаем, что количество подъёмов составляет 10 штук, ступеней — 9 штук. Если лестница изготавливается в единичном экземпляре, можно расчётным путём определить, проём в потолке, чтобы человек ростом 2 метра, свободно поднялся на этаж. Опытный мастер-строитель рассчитывает П-образную лестницу по трём величинам, величине проема, высоте потолка, толщине перекрытия.
Важно подсчитать количество ступеней, 1600:160=10 ступеней на марше, фактически это 9 ступеней, так как первая-последняя ступень являются поверхностью пола. Балясины устанавливаются на каждой ступени, шаг балясин на балюстраде составляет 200 — 250 мм.
Видео удалено.| Видео (кликните для воспроизведения). |
Источники:
- Буга, П. Г. Гражданские, промышленные и сельскохозяйственные здания / П.Г. Буга. — М.: Альянс, 2011. — 352 c.
- Сугак, Е.
 Б. Безопасность жизнедеятельности (раздел «Охрана труда в строительстве»). Учебное пособие / Е.Б. Сугак. — М.: НИУ МГСУ, 2016. — 112 c.
Б. Безопасность жизнедеятельности (раздел «Охрана труда в строительстве»). Учебное пособие / Е.Б. Сугак. — М.: НИУ МГСУ, 2016. — 112 c. - Основин В. Н., Шуляков Л. В., Дубяго Д. С. Справочник по строительным материалам и изделиям; Феникс — Москва, 2008. — 448 c.
Расчет п образной лестницы
Оценка 5 проголосовавших: 1Приветствую Вас на нашем портале. Меня зовут Михаил Суханов. Я уже более 6 лет занимаюсь строительством. Я считаю, что являюсь профессионалом в своей области, хочу научить всех посетителей сайта решать сложные и не очень задачи.
Все материалы для сайта собраны и тщательно переработаны с целью донести как можно доступнее всю необходимую информацию. Однако чтобы применить все, описанное на сайте всегда необходима обязательная консультация с профессионалами.
деревянные конструкции с забежными ступенями на 180 градусов, расчет оптимального подъема на второй этаж, размеры для частного дома
Лестничные конструкции в форме буквы «П» смотрятся интересно и оригинально. Их устанавливают во многих частных домах. Но в обустройстве подобной конструкции есть ряд своих нюансов, касаемых проектирования, материала и других важных аспектов. Поэтому прежде чем решить устанавливать сооружение данного типа, нужно внимательно ознакомиться со всеми особенностями выбора и монтажа конструкции.
Их устанавливают во многих частных домах. Но в обустройстве подобной конструкции есть ряд своих нюансов, касаемых проектирования, материала и других важных аспектов. Поэтому прежде чем решить устанавливать сооружение данного типа, нужно внимательно ознакомиться со всеми особенностями выбора и монтажа конструкции.
Особенности
П-образная лестница представляет собой конструкцию, чаще всего состоящую из трех маршей. Ее особенностью является способность одного марша изменить направление шага. Такие конструкции еще называют поворотными. Средний марш обязательно должен включать в себя несколько ступеней, а иногда и площадку.
Лестничное сооружение с поворотом может иметь следующие типы конструкции:
- Вариант с забежными ступенями подразумевает наличие в поворотном марше как минимум шести ступенек, расположенных под определенным углом.
 Плюсом подобных сооружений является их большая компактность по сравнению с площадочными конструкциями.
Плюсом подобных сооружений является их большая компактность по сравнению с площадочными конструкциями. - Не менее популярна модель со специальной площадкой под поворот. Такая лестница гораздо более габаритна, но в тоже время, она удобнее в использовании. С помощью данного сооружения можно создать нишу для хранения различных вещей. Она как раз должна располагаться под поворотной площадкой.
Важной характеристикой для установки подобного типа лестницы является ее направление. Она может иметь заход слева или справа. Этот критерий определяется непосредственно владельцами частного дома исходя из особенностей планировки помещения.
Важно спланировать наличие или отсутствие подступенок в конструкции. Если их нет, то сооружение считается лестницей открытого типа, а если есть, то конструкция относится к закрытому типу. Очень часто данный фактор зависит от материала, из которого сделана лестница. Если металлический каркас подразумевает открытость подступеней, то в случае с древесиной они чаще всего закрыты.
Если их нет, то сооружение считается лестницей открытого типа, а если есть, то конструкция относится к закрытому типу. Очень часто данный фактор зависит от материала, из которого сделана лестница. Если металлический каркас подразумевает открытость подступеней, то в случае с древесиной они чаще всего закрыты.
Еще один необычный нюанс – наличие в данной конструкции особой пригласительной ступени, которая отличается по параметрам от всех остальных ступенек. Данная деталь придает лестнице более презентабельный вид, но в некоторых стилях интерьера вполне можно обойтись и без нее.
Отмечается также, что наружная сторона поступи у подобных сооружений должна быть больше, чем внутренняя. Данная особенность позволяет наиболее комфортно и безопасно пользоваться лестницей, поскольку имеется надежная опора ля стопы.
Данная особенность позволяет наиболее комфортно и безопасно пользоваться лестницей, поскольку имеется надежная опора ля стопы.
Плюсы и минусы
Лестница с разворотом имеет как положительные, так и отрицательные черты, которые следует учесть заблаговременно. К преимуществам подобной лестницы относятся:
- Оригинальный вид. Данное сооружение действительно смотрится нестандартно. Оно может стать прекрасным акцентным элементом в интерьере прихожей.
- Благодаря разнообразию использования допустимых материалов П-образная лестница станет уместной для многих классических и современных стилей интерьера.
- Эксплуатация подобных лестниц является вполне безопасной, если конструкции оснащены перилами и балясинами.
Среди отрицательных сторон выделяют следующие:
- Данные сооружения занимают достаточно много места.
 Они могут быть установлены только в просторных частных домах или общественных сооружениях с высокими потолками. Кроме того, П-образные лестницы требуют довольно большого количества материала для своего сооружения, что может сильно отразиться на финансовой стороне вопроса.
Они могут быть установлены только в просторных частных домах или общественных сооружениях с высокими потолками. Кроме того, П-образные лестницы требуют довольно большого количества материала для своего сооружения, что может сильно отразиться на финансовой стороне вопроса. - Винтовая конструкция такого типа предлагает довольно значительное сужение ступеней с одной стороны, бывает сложно выверить необходимый баланс для максимального удобства эксплуатации.
- Сам монтаж такой лестничной конструкции – не очень легкий процесс. Он под силу только опытным мастерам. Новичок самостоятельно не справится с сооружением и установкой лестницы такого типа.
Чтобы не запутаться в плюсах и минусах сооружения, главное – рассчитать свой бюджет и учесть все особенности дома, где планируется устанавливать поворотную лестницу.
Как рассчитать?
Если вы решили самостоятельно осуществить монтаж П-образного лестничного сооружения, то важным этапом этого процесса станет расчет всех параметров будущей конструкции между этажами. Прежде всего, нужно учесть угол поворота планируемой конструкции.
Существуют сооружения с более резким и плавным углом:
- Угол в 180 градусов подразумевает использование забежных ступеней. Для данного сооружения очень важна безопасность, поэтому ширина даже в самом узком месте она ступень должна быть более 10 см, а проступь может нависать на 5 см. Между двумя маршами должен быть промежуток размером в четверть ширины одного марша. При достаточном количестве прямых ступеней переходы на лестничной конструкции подобного типа становятся менее заметными.

- Угол в 80 градусов подразумевает более плавные линии изгиба в самой конструкции, поэтому в данном случае нет необходимости создавать дополнительные мягкие переходы в линиях самих ступеней.
Помните, что длина поворотного марша должна быть не менее двух метров. Уклон данного марша должен быть не более 45 градусов. В противном случае возникнут неудобства особенно при эксплуатации лестницы маленькими детьми или пожилыми людьми.
Важно также учитывать ширину поступи. При ее расчете важно принимать во внимание самый большой размер ступни среди жителей помещения. Оптимально, чтобы ширина не была менее 25 сантиметров.
В П-образных лестницах важно рассчитывать, сколько ступеней должно находиться как до, так и после поворотной части сооружения или площадкой. Данное количество устанавливается следующим образом:
Данное количество устанавливается следующим образом:
- Нужно измерить точную высоту пространства между первым и вторым этажом. В эту высоту должна включаться также высота межэтажного перекрытия и слоя отделочного материала.
- Данную величину затем нужно делить на высоту подступенка.
- Если в результате не получается целого числа, например, результатом станет показатель в 12, 7, то следует соорудить 12 ступеней, а оставшуюся часть использовать для пригласительной ступени.
- Чтобы схема строения лестницы и чертеж проекта были максимально точными, рекомендуется производить расчеты с помощью специальных программ и калькуляторов.
- Если вы решили создать лестницу с забежными ступенями, то целесообразно воспользоваться следующими способами расчета:
- Использование оси координат подразумевает размещение по оси X высоты подступенок, в то время как по оси Y будет размещаться ширина ступени.
 Поворотный марш нужно выделить на чертеже окружностью, разделить на одинаковые секторы, а затем перенести на проекцию. При этом необходимо учитывать все особенности данной схемы и наиболее подходящие величины.
Поворотный марш нужно выделить на чертеже окружностью, разделить на одинаковые секторы, а затем перенести на проекцию. При этом необходимо учитывать все особенности данной схемы и наиболее подходящие величины. - При использовании пропорции основные ступени размещаются равномерно относительно поворотных. По смещенной к центру поворота маршевой средней линии располагаются поворотные ступени. В основу расчетов положена ширина поступи в самом узком месте и в месте, где стороны степеней пересекаются со средней маршевой линией.
При установке в частном доме двухмаршевой лестничной конструкции с площадкой, помните, что от угла поворота будет зависеть форма самой площадки.
А в следующем видеоролике можно посмотреть, как произвести замеры для расчета П-образной лестницы.
Используемые материалы
Для создания подобных лестничных конструкций используется широкий спектр материалов. Среди них можно увидеть следующие варианты:
- Деревянные лестницы очень популярны для многих стилей интерьера. Плюс подобных конструкций в том, что предоставляется богатый выбор сортов древесины. Самыми надежными и прочными из них считают дуб и бук. Также большим спросом пользуется ясень. Бюджетной альтернативой станут хвойные деревья, но срок их эксплуатации существенно короче.
- Металлические варианты чаще всего реализуются в виде конструкций без подступенок.
 Они являются довольно прочными, но в помещениях с высоким уровнем влажности лучше не устанавливать сооружения из подобного материала, или обрабатывать их специальными средствами от коррозии.
Они являются довольно прочными, но в помещениях с высоким уровнем влажности лучше не устанавливать сооружения из подобного материала, или обрабатывать их специальными средствами от коррозии.
- Бетонные лестницы П-образной формы являются цельными монолитными конструкциями, привлекающими к себе внимание.
- Стекло, напротив, выглядит более невесомо и изящно. Недостатком подобных конструкций является их хрупкость, также стеклянные поверхности могут быть скользкими, что весьма травмоопасно. Поэтому из данного материала лучше сооружать отдельные лестничные элементы, например, перила.
- Помимо перечисленных материалов, можно встретить комбинированные варианты, предполагающие в основном сочетание двух разных материалов.
 Часто в качестве каркаса лестницы используется металл, а ступени делаются из древесины.
Часто в качестве каркаса лестницы используется металл, а ступени делаются из древесины.
Конструкции такого типа редко создаются из камня.
Как изготовить самостоятельно?
Самому П-образную легче всего сделать и собрать из древесины. Этот материал довольно часто используется и легко поддается различного рода обработке.
При изготовлении лестницы своими руками нужно следовать пошаговой инструкции:
- Важно запастись всеми необходимыми деталями из дерева. К ним относятся: брус, доски, специальный герметизирующий клей.
- Из инструментов вам понадобятся: шуруповерт, топор, саморезы, перфоратор, уровень, молоток, электрическая дрель, топор.

- Первым делом необходимо тщательно просушить древесину.
- Затем ее обрабатывают специальными пропитками, защищающими материал от воздействия воды, а также различных паразитов и грибковых образований.
- Из бруса сооружается несущий косоур. Помните, что длина должна быть равна длине одного марша.
- Чтобы создать ступени конструкции, понадобятся доски одинакового размера. Также равными по размеру должны быть подступенки и поступи.
- Чтобы закрепить каркас ступеней, необходимо воспользоваться такими крепежными элементами, как саморезы.
- Балясины и поручни можно создать самостоятельно, если у вас есть достаточный опыт в подобных работах. Но новичкам рекомендуется приобрести уже готовые детали подобного типа.
- Чтобы избавиться от неровностей на стыках или мелких щелей, данные недостатки необходимо скорректировать с помощью клея-герметика.
- После этого лестница должна быть покрыта прозрачным или декоративным лаком.
Если следовать представленному алгоритму, то получится правильно соорудить П-образную лестничную конструкцию.
Полезные советы
Обращайте особое внимание на марш, который является поворотным, или на площадку. Обязательно ограждайте его перилами, которые обеспечат дополнительную безопасность подъема и спуска.
Если в вашей семье проживает человек с ограниченными возможностями, следует воздержаться от установки подобной лестницы. Из-за кривизны ступеней и сложности конструкции, на лестницу сложно установить пандус. Чтобы удобнее было высчитывать необходимые параметры будущей лестницы, целесообразно воспользоваться формулой Блонделя.
Красивые примеры в интерьере
Межэтажная лестница может быть интересно оформлена в загородном доме:
- Весьма оригинально П-образная конструкция смотрится в сочетании с подсветкой. Она может быть как линейной, так и точечной, бросающей свет лишь на отдельные участки ступеней.
- Ступени, подступенки, перила и балясины могут быть оформлены в контрастном сочетании. Такой вариант придаст конструкции броскости и позволит ей выполнять акцентную роль в интерьере.
- Использование цветного стекла придаст лестничной конструкции легкости, наполнит интерьер элегантностью.
Чтобы ваш дом украшала потрясающая лестничная конструкция с П-образным силуэтом, важно осознанно отнестись к выбору материалов, монтажу и расчетам конструкции. Именно в таком случае лестница станет не только красивым, но также удобным и функциональным элементом интерьера.
Сегодняшним дачникам, желающим построить лестницу в своем доме очень повезло: им в помощь появились современные инструменты, позволяющие рассчитать параметры будущей лестницы самостоятельно. Самодеятельному строителю не нужно изучать стопку книг с инструкциями или искать логарифмическую линейку для расчетов – для расчета лестницы и построения ее рабочих чертежей достаточно открыть онлайн-калькулятор лестниц. Предлагаем изучить возможности и принципы работы калькулятора дял расчета лестниц. Рассчитаем для примера «Дачную лестницу». Это типовая Г-образная деревянная лестница с упрощенным алгоритмом – специально для расчета лестницы обычным дачником. Введем следующие размеры (рис.1, шаг 2): высоту вашего помещения, ширину и длину проема, отведенного под лестницу. Жмем внизу «Рассчитать» (шаг 3) – и в окошке справа получаем результат: чертеж лестницы (вид сверху), которая идеально впишется в ваш дом. Проверяем результаты и если все верно – жмем кнопку «Чертеж» (шаг 4). Рисунок 1. Он-лайн расчет типовой Г-образной деревянной лестницы. |
Программой рассчитывается и открывается в отдельном окне полный чертеж рассчитываемой онлайн лестницы (рис.2) – со всеми установочными размерами, высотой ступенек, наступной шириной лестницы и прочими параметрами, необходимыми для изготовления лестницы своими руками. Рисунок 2. Схема и чертеж лестницы при расчете с помощью онлайн калькулятора. |
|
С помощью онлайн калькулятора можно расчитать и более сложные вариант лестниц для дома. Для примера рассчитаем П-образную лестницу (рис.3). Выбираем в калькуляторе тип лестницы – «П-образная лестница». Здесь алгоритм расчета немного сложнее: вам нужно вводить параметры не помещения, а самой лестницы (рис.3, шаг1): ее высоту, ширину прохода лестницы; в сочетании с любым количеством ступеней (программа сама сразу подсчитывает высоту подъема каждой ступени). Указав параметры, нажимаем кнопку «Рассчитать» и получаем в правом окне результат – вид лестницы сверху. Вы можете добавить ограждение к лестнице – справа или слева, ограждение всей лестницы внутри ее поворота, снаружи, либо ограждение только одного ее пролета. Рисунок 3. Расчет П-образной лестницы с помощью онлайн калькулятора. |
|
Жмем на кнопку «Дизайн» (рис. 3, шаг. 2) и выбираем цвет будущей лестницы, дизайн балясин лестницы, заходных столбов и поручней (под знаком «?» можно посмотреть картинки-подсказки) (рис. 4). Особое значение для стоимости будущей лестницы играет материал, из которого будут изготавливаться детали лестницы. Вы можете выбрать, например, ступеньки из дуба, а все остальные детали лестницы – из более экономичных материалов (сосны или березы). Выбрав нужный дизайн, материал, цвет лестницы, жмем «Рассчитать» и кнопку «Чертеж». Рисунок 4. Выбор материала для лестницы с помощью онлайн калькулятора. |
|
Онлайн-калькулятор лестниц позволяет рассчитать и более сложные виды лестниц: например, винтовую лестницу (рис.5). Вы можете «поиграть» с различными параметрами лестниц сами. Например, чем больше «закрутить» винтовую лестницу (например, до 270°, а лучше до 360°), то лестница получится более удобная – с широкими ступенями. Расчет винтовой лестницы аналогичен всем остальным типам лестниц. Рисунок 5. Он лайн расчет винтовой лестницы с помощью калькулятора. |
|
Особо хочется заострить внимание читателей на расчете прямой лестницы (рис.6). Здесь алгоритм расчета упрощен и аналогичен дачной лестнице. Вам достаточно ввести параметры своего помещения – а программа сама рассчитает лестницу, которая идеально впишется в такой дом. Рисунок 6. Расчет прямой лестницы с помощью онлайн калькулятора. |
|
Более того, если проем слишком мал (см. рис.7: длина проема всего лишь 2м 30 см), то программа предложит вам установить «лестницу с гусиным шагом» как самую малогабаритную. Введя свои параметры, не забывайте жать на кнопку «Рассчитать лестницу» и далее на «Чертеж лестницы», чтобы увидеть результат. Полученные чертежи можно распечатать (Ctrl+P) и использовать при изготовлении или заказе будущей лестницы. Рисунок 7. Расчет лестницы «гусиный (утиный) шаг» с помощью онлайн калькулятора. |
|
Особенность калькулятора лестниц состоит в том, что он разработан для расчета именно деревянных лестниц и учитывает все детали конструктива (место под тетиву лестницы, ее ограждение; конструктив забежных ступеней из дерева и т.д.). В отличие от него другие онлайн-инструменты рассчитают лестницу независимо от материалов: будь это лестницы из бетона либо металлические лестницы. Даже если у вас нет опыта столяра-лестничника, но вам нужно рассчитать, какая лестница хорошо станет в доме или вы даже хотите изготовить ее сами – онлайн-калькулятор лестницы позволит в считанные минуты учесть все параметры и даже распечатать чертежи. Вам остается только заказать ее у производителей лестниц или изготовить лестницу самому. |
Расчет металлической лестницы с тетивой зигзаг
П-образная лестница является достаточно удобной и практичной из-за наличия поворотной площадки П-образная лестница имеет поворотную площадку на 180 градусов. Такая конструкция достаточно удобная для людей любого возраста и занимает мало места в помещении. Чтобы подъем был удобен, необходимо делать угол наклона лестницы от 30ᵒ до 40ᵒ, тогда можно будет безопасно подниматься, как пожилым людям, так и маленьким деткам.
Материалы для П-образных лестниц на второй этаж дома
Конструкция лестницы изготавливается из любого доступного материала.
Для изготовления лестницы для загородного дома лучше использовать ценную породу древесины
А именно:
- Из дерева крепких пород – зачастую, для подобных целей, чаще всего, используется дуб. Подобный материал удобен тем, что он легко обрабатывается, и имеется в достаточном количестве в любом строительном супермаркете.
- Из металла – очень красиво и дорого смотрится ковка, сделанная профессионалом. Она не только будет придавать комнате завершенный вид, и облагораживать помещение, но и прослужит не один десяток лет.
- Бетонные лестницы являются наименее затратными, но они не создают ощущения уюта и теплоты, а лишь ассоциацию с подъездной площадкой.
- Плитка и ламинат используются довольно редко, ведь главным правилом создания лестниц является гармония с окружающим пространством, а при применении подобного материала, конструкция может сливаться с полом, и создавать дисгармонию.
Также можно применять комбинацию двух или нескольких материалов между собой. Это позволит создать интересное и оригинальное творение, подчеркивающее стиль помещения и быть достаточно удобным.
Виды П-образных лестниц с площадкой и без
Существует 2 вида лестниц, имеющих П-образную форму.
А именно:
- С наличием забежных поворотных ступеней – при подобной планировке вместо площадки прикрепляются несколько дополнительных ступенек, они создают небольшой виток и позволяют перестроиться человеку на продолжение подъема. Подобные чертежи и созданная по ним лестница будет менее удобной для пожилых людей и детей, поэтому необходимо учитывать этот фактор, разрабатывая ее размеры в режиме онлайн, а затем воплощая их в жизнь. Ширина ступеней в подобной конструкции должна быть в наиболее узком месте – от 10 см, а в самой широкой – более 25 см. Если изготовление лестницы происходит своими руками, то могут возникнуть проблемы во время правильной нарезки ступеней, поэтому перед началом работы, лучше проконсультироваться со специалистом, чтобы не испортить дорогостоящий материал.
- С наличием площадки – подобные конструкции чаще всего встречаются в домах, и объясняется подобный расчет тем, что они являются наиболее комфортными для всех членов семьи, независимо от возраста. Единственным минусом их в частном доме является то, что они занимают достаточное количество свободного места, и, соответственно, на их сооружение потребуется больший расход стройматериалов.
Существуют П-образные лестницы как с площадкой, так и без, поэтому только вам решать какую выбирать
Какую выбрать П-образную лестницу, с наличием площадки или без нее, решать только владельцу.
Но, делая подобный выбор, нужно учитывать и определенные факторы – наличие достаточного количества денежных средств не только на покупку стройматериалов, но и на оплату работникам при установке, количество членов семьи, проживающих в доме и их средняя весовая категория.
Если в доме есть инвалиды или люди с определенными проблемами со здоровьем, это также нужно учитывать, ведь не всегда можно вовремя прийти им на помощь.
Особенности расчета при проектировании забежных лестниц
Наиболее сложные в реализации и расчётах проекты с забежными ступенями. Любая поворотная бетонная лестница на 180 или 90 градусов требует строго соблюдения нормативов, и их нарушение сделает неудобной её дальнейшую эксплуатацию. Для таких проектов существуют общие требования, которые гарантируют высокий уровень безопасности и стали нормой при проектировании.
- Ширина забежной ступени не должна быть более 40 см в широкой части и 10 см в узкой части.
- Высота каждой ступени рассчитывается в пределах от 12 до 22 см.
- Максимальный выступ края проступи не может превышать 40 см.
- Средняя часть каждой ступени должна быть более 20 см.
Следует учесть, что число забежных ступеней должно быть оптимальным для безопасного передвижения. Для всех типов лестниц актуальна минимальная ширина не менее 80 см. Детальный расчёт забежных лестниц зависит от угла поворота и конструктивных особенностей здания.
Правила безопасности для лестниц на 180 градусов
Наиболее правильным вариантом является заказ лестницы в специализированной фирме.
Профессионал приедет на место, и сделает необходимые замеры, создаст чертеж на компьютере и подкорректирует его под требования хозяев.
Чтобы не натолкнуться на недобросовестного производителя, и получить в результате привлекательную и удобную конструкцию, необходимо придерживаться ряда правил.
Для того чтобы П-образная лестница была безопасной и надежной, лучше обратиться за помощью к специалистам
А именно:
- Лестницу на 180 градусов делают в наиболее редких случаях, если действительно не хватает места на более объемную и безопасную конструкцию, чтобы по ней можно было быстро передвигаться.
- Отдавать предпочтение известной фирме, имеющей много хороших отзывов.
- Перед тем, как взять предварительный платеж, фирма должна приехать на место и сделать предварительные замеры, и создать онлайн-проект лестницы. Если подобную работу накладывают на владельца, лучше отказаться от их услуг, ведь даже малейшая ошибка в замере может понести за собой много нюансов, и человек получит в результате финансовый ущерб и неудобную или неправильно сделанную конструкцию.
- После установки, необходимо обязательно протестировать лестницу – пройдясь по ней, пробежав по ней, и чтобы не было слышно скрипа, пошатывания, или узких ступенек.
При любых неполадках, нужно обязательно требовать их устранения на месте, чтобы в дальнейшем это не привело к трагическим последствиям.
Калькулятор металлических лестниц
В ходе проектирования любой лестницы необходимо обязательно учитывать множество различных параметров, оказывающих влияние на целостность всей конструкции. Особое же внимание при расчете подобного сооружения, прежде всего, следует уделять таким элементам, как пролеты, марши, ступени и, конечно же, ограждения.
Процедура планировки лестницы должна полностью исключать даже самые незначительные ошибки, поскольку это, в последствие, может привести к очень серьезным неприятностям. При этом наиболее высокую точность очень важно соблюдать при сооружении именно металлических лестниц, так как осуществлять подгонку ее элементов под необходимые размеры, в случае какой-либо ошибки при расчете, будет весьма затруднительно.
Чтобы произвести расчет металлической лестницы онлайн, воспользуйтесь соответствующим калькулятором:
- Калькулятор прямой металлической лестницы
- Калькулятор металлической лестницы с тетивой типа зигзаг
- Калькулятор металлической лестницы с поворотом на 90 градусов
- Калькулятор металлической лестницы с поворотом на 90 градусов и тетивой типа зигзаг
- Калькулятор металлической лестницы с поворотом на 180 градусов
- Калькулятор металлической лестницы с поворотом на 180 градусов и тетивой типа зигзаг
Работы по проектированию подобных конструкций необходимо обязательно с расчета самой лестничной площадки. Данные элементы у лестниц чаще всего выполняются в прямоугольных формах, хотя, конечно же, случаются и исключения. В ходе проектирования будущей лестницы, очень важно опираться на ее предполагаемый угол наклона, что поможет добиться более точных результатов. Еще одно довольно важное правило при расчете металлических лестниц заключается в том, что ширина марша у таких конструкций, должна обязательно быть аналогичной или же чуть меньшей, чем ширина у самой площадки.
Проектирование лестниц с несколькими маршами осуществляется по абсолютно тем же правилам, правда, с учетом ряда определенных нюансов. Так, например, уровень марша у таких конструкций должен строго соответствовать высоте ступеней, а сами марши должны обязательно смотреть только водном направлении.
Что касается расчета полностью прямых или изогнутых лестниц, то тут, как правило, применяются несколько иные правила. Непосредственно сами марши у таких конструкций должны обязательно располагаться ни как не реже чем через девять-десять ступенек. Кроме того, тут также очень важно учитывать защитные ограждения и, конечно же, сами опорные конструкции. Ведь кроме эстетической составляющей, такая достаточно важная деталь лестницы, как перила, также служат еще и элементом безопасности, а значит, их правильный расчет невероятно важен.
Для изготовления лестничных перил желательно подбирать материалы, отличающиеся повышенным показателем прочности, такие как, например, алюминий или сталь. Сами же покрытия, в данной ситуации, вполне можно будет сделать уже из пластика или дерева.
Похожие записи
Калькулятор фундаментной плиты
Онлайн калькулятор ленточного фундамента
Калькулятор расчета гипсокартона
Калькулятор прямой бетонной лестницы
Советы по онлайн-расчету П-образной лестницы от специалистов
Чтобы произвести правильный расчет схемы и материалов для лестницы частного дома, необходимо соблюдение нескольких правил.
Перед изготовлением и установкой П-образной лестницы, следует правильно произвести расчеты как конструкции, так и помещения
А именно:
- Просчитывать размеры, необходимо опираясь на параметры среднестатистического человека. Существует 3 формулы – безопасности, удобства и шага. Каждая является важным соло в формуле, поэтому пренебрегать ими не стоит. Готовая конструкция, сделанная по правилам, будет не только радовать глаз хозяев, но и удобной, комфортной не только для ходьбы, но и переноски вещей.
- Высота перил должна составлять не менее 90-95 см, а количество балясин должно совпадать с количеством ступеней или более, расстояние – не более 55 см.
- Наиболее комфортной шириной марша является 90 см.
- Чтобы не доставлять дискомфорта высоким людям, высота от ступеней до потолка должна быть не менее 2 м.
- Перила должны быть изготовлены из материала, который бы не доставлял дискомфорта во время подъема – древесина должна быть идеально отполирована, зашлифована и покрыта лаком или краской, металл лучше покрыть специальными накладками, чтобы в зимнее время рукам не было холодно, ведь особенно неприятно это для пожилых людей и детей.
- На ступени лучше положить специальные ковровые покрытия, с наличием клейкой внутренней стороны или крепежа. Это позволит снимать их для уборки и быть безопасными во время бега или передвижения.
- Цветовая гамма лестницы, ковриков и общего стиля комнаты должны совпадать и гармонично сочетаться между собой, тогда у вошедшего в комнату человека не будет создаваться впечатления незавершенности или перебора в дизайне.
- Красиво смотрятся кованые балясины, на выбор дизайнера, они могут быть, как покрашены однотонной краской, так и добавлены некоторые мазки бронзой, позолотой или легкие переливы серебра.
- Древесина также не будет скучной, если в арсенале дизайнера или хозяина присутствует фантазия и желание преобразить лестничную конструкцию – множество резных элементов способны превратить обычную балясину в произведение искусства. Это будет гармонично смотреться в стиле барокко, и незаменимо в классическом интерьере.
Подчеркнут дороговизну и шик творения красные ковровые накладки, превращающие обычную лестницу в ковровую дорожку. Единственным минусом этого творения является его стоимость – зачатую, она обходится довольно дорого, ведь, в основном, применяется ручная работа, что является залогом ценности и оригинальности.
Расчет бетонных лестниц с поворотом на 90 и 180 градусов
В зависимости от выбранного проекта такое сооружение может иметь П-образное или Г-образное исполнение. Чтобы выполнить расчёт бетонной лестницы с поворотом на 180 градусов, следует отметить центральную точку изгиба (A), которая будет совпадать с внутренним радиусом забежных ступеней. Далее, необходимо провести линию (DE), соединяющую первую и последние забежные ступени и проложить ось (CD) перпендикулярную проведённой ранее линии. Чтобы провести дальнейший расчёт необходимо проложить кривую по центру лестничного марша, пересечение которой с осью (CD) и будет началом отсчёта. От этой точки откладывается отрезок в половину размера ступени, а дальнейшая разметка производится с учётом всей ширины ступени.
Расчёт лестницы с поворотом на 90 градусов схож разметкой с П-образной конструкции, только здесь ось проходит по точке излома лестницы и делит место поворота по диагонали на два угла в 45 градусов. Отсутствие навыков работы с чертежами может затруднить выполнение таких подсчётов и обратиться в нашу компанию будет верным решением. Произвести расчет бетонной лестницы с поворотом в Москве достаточно просто, опытные специалисты сделают точный проект, а монтаж займет минимально возможное количество времени.
Дизайн П-образной лестницы (фото интерьера)
на второй этаж с площадкой, 180 градусов, онлайн-расчет своими руками, размеры и фото
П-образная лестница является достаточно удобной и практичной из-за наличия поворотной площадки
П-образная лестница имеет поворотную площадку на 180 градусов. Такая конструкция достаточно удобная для людей любого возраста и занимает мало места в помещении. Чтобы подъем был удобен, необходимо делать угол наклона лестницы от 30ᵒ до 40ᵒ, тогда можно будет безопасно подниматься, как пожилым людям, так и маленьким деткам.Содержание материала:
Материалы для П-образных лестниц на второй этаж дома
Конструкция лестницы изготавливается из любого доступного материала.
Для изготовления лестницы для загородного дома лучше использовать ценную породу древесины
А именно:
- Из дерева крепких пород – зачастую, для подобных целей, чаще всего, используется дуб. Подобный материал удобен тем, что он легко обрабатывается, и имеется в достаточном количестве в любом строительном супермаркете.
- Из металла – очень красиво и дорого смотрится ковка, сделанная профессионалом. Она не только будет придавать комнате завершенный вид, и облагораживать помещение, но и прослужит не один десяток лет.
- Бетонные лестницы являются наименее затратными, но они не создают ощущения уюта и теплоты, а лишь ассоциацию с подъездной площадкой.
- Плитка и ламинат используются довольно редко, ведь главным правилом создания лестниц является гармония с окружающим пространством, а при применении подобного материала, конструкция может сливаться с полом, и создавать дисгармонию.
Также можно применять комбинацию двух или нескольких материалов между собой. Это позволит создать интересное и оригинальное творение, подчеркивающее стиль помещения и быть достаточно удобным.
Виды П-образных лестниц с площадкой и без
Существует 2 вида лестниц, имеющих П-образную форму.
А именно:
- С наличием забежных поворотных ступеней – при подобной планировке вместо площадки прикрепляются несколько дополнительных ступенек, они создают небольшой виток и позволяют перестроиться человеку на продолжение подъема. Подобные чертежи и созданная по ним лестница будет менее удобной для пожилых людей и детей, поэтому необходимо учитывать этот фактор, разрабатывая ее размеры в режиме онлайн, а затем воплощая их в жизнь. Ширина ступеней в подобной конструкции должна быть в наиболее узком месте – от 10 см, а в самой широкой – более 25 см. Если изготовление лестницы происходит своими руками, то могут возникнуть проблемы во время правильной нарезки ступеней, поэтому перед началом работы, лучше проконсультироваться со специалистом, чтобы не испортить дорогостоящий материал.
- С наличием площадки – подобные конструкции чаще всего встречаются в домах, и объясняется подобный расчет тем, что они являются наиболее комфортными для всех членов семьи, независимо от возраста. Единственным минусом их в частном доме является то, что они занимают достаточное количество свободного места, и, соответственно, на их сооружение потребуется больший расход стройматериалов.
Существуют П-образные лестницы как с площадкой, так и без, поэтому только вам решать какую выбирать
Какую выбрать П-образную лестницу, с наличием площадки или без нее, решать только владельцу.
Но, делая подобный выбор, нужно учитывать и определенные факторы – наличие достаточного количества денежных средств не только на покупку стройматериалов, но и на оплату работникам при установке, количество членов семьи, проживающих в доме и их средняя весовая категория.
Если в доме есть инвалиды или люди с определенными проблемами со здоровьем, это также нужно учитывать, ведь не всегда можно вовремя прийти им на помощь.
Правила безопасности для лестниц на 180 градусов
Наиболее правильным вариантом является заказ лестницы в специализированной фирме.
Профессионал приедет на место, и сделает необходимые замеры, создаст чертеж на компьютере и подкорректирует его под требования хозяев.
Чтобы не натолкнуться на недобросовестного производителя, и получить в результате привлекательную и удобную конструкцию, необходимо придерживаться ряда правил.
Для того чтобы П-образная лестница была безопасной и надежной, лучше обратиться за помощью к специалистам
А именно:
- Лестницу на 180 градусов делают в наиболее редких случаях, если действительно не хватает места на более объемную и безопасную конструкцию, чтобы по ней можно было быстро передвигаться.
- Отдавать предпочтение известной фирме, имеющей много хороших отзывов.
- Перед тем, как взять предварительный платеж, фирма должна приехать на место и сделать предварительные замеры, и создать онлайн-проект лестницы. Если подобную работу накладывают на владельца, лучше отказаться от их услуг, ведь даже малейшая ошибка в замере может понести за собой много нюансов, и человек получит в результате финансовый ущерб и неудобную или неправильно сделанную конструкцию.
- После установки, необходимо обязательно протестировать лестницу – пройдясь по ней, пробежав по ней, и чтобы не было слышно скрипа, пошатывания, или узких ступенек.
При любых неполадках, нужно обязательно требовать их устранения на месте, чтобы в дальнейшем это не привело к трагическим последствиям.
Советы по онлайн-расчету П-образной лестницы от специалистов
Чтобы произвести правильный расчет схемы и материалов для лестницы частного дома, необходимо соблюдение нескольких правил.
Перед изготовлением и установкой П-образной лестницы, следует правильно произвести расчеты как конструкции, так и помещения
А именно:
- Просчитывать размеры, необходимо опираясь на параметры среднестатистического человека. Существует 3 формулы – безопасности, удобства и шага. Каждая является важным соло в формуле, поэтому пренебрегать ими не стоит. Готовая конструкция, сделанная по правилам, будет не только радовать глаз хозяев, но и удобной, комфортной не только для ходьбы, но и переноски вещей.
- Высота перил должна составлять не менее 90-95 см, а количество балясин должно совпадать с количеством ступеней или более, расстояние – не более 55 см.
- Наиболее комфортной шириной марша является 90 см.
- Чтобы не доставлять дискомфорта высоким людям, высота от ступеней до потолка должна быть не менее 2 м.
- Перила должны быть изготовлены из материала, который бы не доставлял дискомфорта во время подъема – древесина должна быть идеально отполирована, зашлифована и покрыта лаком или краской, металл лучше покрыть специальными накладками, чтобы в зимнее время рукам не было холодно, ведь особенно неприятно это для пожилых людей и детей.
- На ступени лучше положить специальные ковровые покрытия, с наличием клейкой внутренней стороны или крепежа. Это позволит снимать их для уборки и быть безопасными во время бега или передвижения.
- Цветовая гамма лестницы, ковриков и общего стиля комнаты должны совпадать и гармонично сочетаться между собой, тогда у вошедшего в комнату человека не будет создаваться впечатления незавершенности или перебора в дизайне.
- Красиво смотрятся кованые балясины, на выбор дизайнера, они могут быть, как покрашены однотонной краской, так и добавлены некоторые мазки бронзой, позолотой или легкие переливы серебра.
- Древесина также не будет скучной, если в арсенале дизайнера или хозяина присутствует фантазия и желание преобразить лестничную конструкцию – множество резных элементов способны превратить обычную балясину в произведение искусства. Это будет гармонично смотреться в стиле барокко, и незаменимо в классическом интерьере.
Подчеркнут дороговизну и шик творения красные ковровые накладки, превращающие обычную лестницу в ковровую дорожку. Единственным минусом этого творения является его стоимость – зачатую, она обходится довольно дорого, ведь, в основном, применяется ручная работа, что является залогом ценности и оригинальности.
П-образные лестницы (видео)
Следуя подобным советам, можно не огорчиться в полученном результате, а наслаждаться комнатой долгое время.
Дизайн П-образной лестницы (фото интерьера)
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Расчет изготовления лестниц — Онлайн-Калькулятор
a:2:{s:4:»TEXT»;s:5601:» Расчет лестниц с нашими специалистами – просто! Планируя отделку и обустройство своего дома, желательно на самом раннем этапе предусмотреть наличие лестницы. Оптимальным решением является случай, при котором лестница является неотъемлемой частью всего проекта. При таком варианте расчет лестницы производиться заранее, она вписывается гармонично в обустраиваемое пространство и отвечает всем потребностям заказчика. Как показывает практика, в большинстве случаев владельцы дома полагаются на рекомендации строителей только отчасти и отводят под лестницу немного места в надежде, что она компактно впишется и будет при этом удобной. Строители или проектировщики, тоже, к сожалению, не всегда уделяют должное внимание такому важному элементу дома, как лестница. Отсюда возникают определенные трудности и ограничения при расчете лестницы. Наши специалисты будут рады помочь с расчетом лестницы на любом этапе строительства и проектирования дома! С чего начать? Мы предлагаем, прежде всего, определиться с размерами необходимыми для расчета лестницы. Для этого можно воспользоваться услугами наших замерщиков или самостоятельно снять замеры следующих параметров: – высота лестницы от пола нижнего этажа до пола верхнего этажа – толщина перекрытия – длина и ширина проема – габариты в плане (длина и ширина площади отводимой под лестницу) – возможные помехи (двери, окна, батареи и т.д.) Далее Нужно определить форму будущей лестницы: http://previous.previous.lestnicy-prosto.ru/catalog/vintovie-lestnici/»>Винтовые лестницыhttp://previous.previous.lestnicy-prosto.ru/catalog/g-obraznye-lestnitsy/»>Г-образные лестницыhttp://previous.previous.lestnicy-prosto.ru/catalog/p-obraznye-lestnitsy/»>П-образные лестницыhttp://previous.previous.lestnicy-prosto.ru/catalog/zabezhnye-lestnitsy/»>Забежные лестницыhttp://previous.previous.lestnicy-prosto.ru/catalog/marshevye-lestnitsy/»>Маршевые лестницы Затем Сделать выбор по материалу: деревянные, на металлокаркасе, металлические. Если лестница деревянная, то нужно определиться с породой: http://previous.previous.lestnicy-prosto.ru/catalog/lestnitsy-iz-sosny/»>Лестницы из сосныhttp://previous.previous.lestnicy-prosto.ru/catalog/lestnitsy-iz-khvoi/»>Лестницы из хвоиhttp://previous.previous.lestnicy-prosto.ru/catalog/lestnitsy-iz-listvennitsy/»>Лестницы из лиственницыhttp://previous.previous.lestnicy-prosto.ru/catalog/lestnitsy-iz-berezy/»>Лестницы из березыhttp://previous.previous.lestnicy-prosto.ru/catalog/lestnitsy-iz-buka/»>Лестницы из букаhttp://previous.previous.lestnicy-prosto.ru/catalog/lestnitsy-iz-yasenya/»>Лестницы из ясеняhttp://previous.previous.lestnicy-prosto.ru/catalog/lestnitsy-iz-duba/»>Лестницы из дубаВ итоге! На основании всех этих данных наш менеджер бесплатно сделает проект, который будет учитывать возможности помещения, исходя из представленных параметров, и все пожелания по комфорту и эстетики вашей будущей лестницы! «;s:4:»TYPE»;s:4:»HTML»;}
Мы настоятельно рекомендуем произвести замер помещения прежде, чем заказывать лестницу. Вы можете вызвать для замера нашего специалиста или самостоятельно произвести замер
Как сделать замер самостоятельно?
Производить замер лучше всего рулеткой с погрешность не более 2-х мм. Если есть возможность, пришлите нам фото помещения в нескольких основных ракурсах.
Замеряя высоты, внимательно следите за тем, чтобы измерительные приборы располагались строго вертикально! Даже небольшое отклонение от вертикали может привести к получению неверных данных.
1 Измерьте длину и ширину проёма для лестницы
Проём — это отверстие в потолке, в которое вы входите, поднимаясь по лестнице, или свободное пространство над головой. Можно сказать, что проём — это проход на верхний этаж в межэтажном перекрытии. Чаще всего проём бывает прямоугольной формы, иногда круглой (в случае винтовых лестниц). Величина проема измеряется либо длиной и шириной, либо диаметром (если речь идёт о круглом проёме для винтовой лестницы).
Бывают случаи, когда лестница «подставляется» к перекрытию верхнего этажа (второй свет). В этом случае измерьте только длину проёма, ширина проёма не здесь ограничена.
У всех лестниц в нашем магазине указан параметр «минимальный проём». Это минимальная величина проёма, комфортная для данной лестницы. Проще говоря, размер проёма должен позволять идущему по лестнице не задевать головой потолок. Если ваш проём не меньше указанного минимального, то лестница вам подходит.
2 Измерьте высоту от пола нижнего этажа до пола верхнего этажа и высоту от пола до потолка
Здесь возможны 2 варианта:
- Ваш пол ещё черновой и чистовым станет позже, когда будут уложены фанера и декоративное покрытие (например, паркетная доска). В таком случае мы рекомендуем при проведении замера учитывать уровень будущего чистового пола или сообщить нам об этом.
- Ваш пол уже чистовой . В этом случае просто зафиксируйте высоты, как показано на картинке ниже.
3 Определите площадь под лестницу на первом этаже
Как это сделать? Вы наверняка уже определили, в каком месте лестница должна начинаться и где должна заканчиваться, и можете обозначить площадь, отводимую под лестницу на нижнем этаже в конкретных цифрах. Не забудьте учесть, что лестница не должна мешать открытию двери или перекрывать окно. Так и определяется площадь, полезная для лестницы, или габариты в плане.
4 Учтите все возможные помехи
Это могут быть двери, окна, батареи, другие особенности помещения. Опишите все нюансы и, если есть возможность, пришлите фотографии в нескольких ракурсах. Если у вас возникли сложности или вопросы, связанные с замером, вы можете совершенно бесплатно проконсультироваться у нашего специалиста.
Пожалуйста, помогите решить проблему со словом ниже
Количество ступенчатых лестниц зависит от количества используемых блоков. Это потому, что без блоков нельзя построить лестницу.
Пусть x = количество блоков
Пусть y = количество ступенек
Создайте таблицу значений для отображения данных.
х | y
__________
1 1
3 2
6 3
Давайте посмотрим, есть ли у этих данных линейная зависимость.Мы делаем это, находя уклон. Уклон между точками 1 и 2 должен иметь уклон между точками 2 и 3.
Наклон 1-3 = (2 — 1) / (3 — 1)
= 1/2
Наклон 2–3 = (3–2) / (6–3)
= 1/3
Наклон не постоянный. Итак, мы знаем, что у нас не будет линейной зависимости.
Итак, теперь нам нужно написать систему линейных уравнений, чтобы найти одно уравнение.Уравнение, которое мы пытаемся получить, является квадратичной функцией. Функция будет иметь вид
у = ах 2 + bx + с
, где a, b и c — константы. Мы подставляем значения x и y из таблицы, чтобы создать эти уравнения.
a + b + c = 1 уравнение 1
9a + 3b + c = 2 экв2
36a + 6b + c = 3 экв3
Заменить eq1 на eq2 и eq3.Получите эти уравнения в терминах a и b.
9a + 3b + (1 — a — b) = 2
8a + 2b = 1 новый eq2
36a + 6b + (1 — a — b) = 3
35a + 5b = 2 новый eq3
Затем умножьте новое уравнение 2 на 5 и умножьте новое уравнение 3 на 2.
40a + 10b = 5 новых eq2
70a + 10b = 4 новых eq3
Затем вычтите новое уравнение 3 из нового уравнения 2, чтобы исключить члены b.
-30a = 1
а = -1/30
Подставьте это значение a в новое уравнение 2, чтобы найти b.
8 (-1/30) + 2b = 1
(-8/30) + 2b = 1
-8 + 60b = 30
60b = 38
b = 19/30
Подставьте значения a и b в уравнение 1, чтобы найти c.
с = 1 — (-1/30) — (19/30)
с = 2/5
Формула, которую мы получаем, когда подключаем a, b и c, равна
.y = (-1/30) x 2 + (19/30) x + (2/5)
онлайн-курсов PDH. PDH для профессиональных инженеров. ПДХ Инжиниринг.
«Мне нравится широта ваших курсов по HVAC; не только экологичность или экономия энергии
курсов.»
Russell Bailey, P.E.
Нью-Йорк
«Он укрепил мои текущие знания и научил меня еще нескольким новым вещам
, чтобы познакомить меня с новыми источниками
информации.
Стивен Дедак, П.Е.
Нью-Джерси
«Материал получился очень информативным и организованным.Я многому научился и их было
очень быстро отвечает на вопросы.
Это было на высшем уровне. Будет использовать
снова. Спасибо. «
Blair Hayward, P.E.
Альберта, Канада
«Простой в использовании веб-сайт. Хорошо организованный. Я действительно буду снова пользоваться вашими услугами.
проеду по вашей компании
имя другим на работе.»
Roy Pfleiderer, P.E.
Нью-Йорк
«Справочные материалы были превосходными, и курс был очень информативным, особенно потому, что я думал, что я уже знаком.
с деталями Канзас
Авария City Hyatt «
Майкл Морган, P.E.
Техас
«Мне очень нравится ваша бизнес-модель.Мне нравится просматривать текст перед покупкой. Нашел класс
информативно и полезно
на моей работе »
Вильям Сенкевич, П.Е.
Флорида
«У вас большой выбор курсов, а статьи очень информативны. You
— лучшее, что я нашел ».
Рассел Смит, П.E.
Пенсильвания
«Я считаю, что такой подход позволяет работающему инженеру легко зарабатывать PDH, давая время на изучение
материал «
Jesus Sierra, P.E.
Калифорния
«Спасибо, что разрешили мне просмотреть неправильные ответы. На самом деле,
человек узнает больше
от сбоев.»
John Scondras, P.E.
Пенсильвания
«Курс составлен хорошо, и использование тематических исследований является эффективным.
способ обучения »
Джек Лундберг, P.E.
Висконсин
«Я очень впечатлен тем, как вы представляете курсы, т.е. позволяете
студент для ознакомления с курсом
материалов до оплаты и
получает викторину.»
Arvin Swanger, P.E.
Вирджиния
«Спасибо за то, что вы предложили все эти замечательные курсы. Я определенно выучил и
получил огромное удовольствие «
Mehdi Rahimi, P.E.
Нью-Йорк
«Я очень доволен предлагаемыми курсами, качеством материалов и простотой поиска.
на связи
курсов.»
Уильям Валериоти, P.E.
Техас
«Этот материал в значительной степени оправдал мои ожидания. По курсу было легко следовать. Фотографии в основном обеспечивали хорошее наглядное представление о
.обсуждаемых тем »
Майкл Райан, P.E.
Пенсильвания
«Именно то, что я искал. Потребовался 1 балл по этике, и я нашел его здесь.»
Джеральд Нотт, П.Е.
Нью-Джерси
«Это был мой первый онлайн-опыт получения необходимых мне кредитов PDH. Это было
информативно, выгодно и экономично.
Я очень рекомендую
всем инженерам »
Джеймс Шурелл, П.Е.
Огайо
«Я понимаю, что вопросы относятся к« реальному миру »и имеют отношение к моей практике, и
не на основании какой-то непонятной секции
законов, которые не применяются
до «нормальная» практика.»
Марк Каноник, П.Е.
Нью-Йорк
«Отличный опыт! Я многому научился, чтобы перенести его на свой медицинский прибор
организация «
Иван Харлан, П.Е.
Теннесси
«Материалы курса имели хорошее содержание, не слишком математическое, с хорошим акцентом на практическое применение технологий».
Юджин Бойл, П.E.
Калифорния
«Это был очень приятный опыт. Тема была интересной и хорошо изложенной,
а онлайн-формат был очень
доступный и простой для
использовать. Большое спасибо ».
Патрисия Адамс, P.E.
Канзас
«Отличный способ добиться соответствия требованиям PE Continuing Education в рамках ограничений по времени лицензиата.»
Joseph Frissora, P.E.
Нью-Джерси
«Должен признаться, я действительно многому научился. Помогает иметь печатный тест во время
обзор текстового материала. Я
также оценил просмотр
фактических случаев «
Жаклин Брукс, П.Е.
Флорида
«Документ» Общие ошибки ADA при проектировании объектов «очень полезен.Модель
испытание потребовало исследований в
документ но ответы были
в наличии «
Гарольд Катлер, П.Е.
Массачусетс
«Я эффективно использовал свое время. Спасибо за широкий выбор вариантов
в транспортной инженерии, что мне нужно
для выполнения требований
Сертификат ВОМ.»
Джозеф Гилрой, П.Е.
Иллинойс
«Очень удобный и доступный способ заработать CEU для моих требований PG в Делавэре».
Ричард Роудс, P.E.
Мэриленд
«Я многому научился с защитным заземлением. Пока все курсы, которые я прошел, были отличными.
Надеюсь увидеть больше 40%
курсов со скидкой.»
Кристина Николас, П.Е.
Нью-Йорк
«Только что сдал экзамен по радиологическим стандартам и с нетерпением жду возможности сдать еще
курсов. Процесс прост, и
намного эффективнее, чем
вынуждены ехать «.
Деннис Мейер, P.E.
Айдахо
«Услуги, предоставляемые CEDengineering, очень полезны для профессионалов
Инженеры получат блоки PDH
в любое время.Очень удобно ».
Пол Абелла, P.E.
Аризона
«Пока все отлично! Поскольку я постоянно работаю матерью двоих детей, у меня мало
время исследовать где на
получить мои кредиты от «
Кристен Фаррелл, P.E.
Висконсин
«Это было очень познавательно и познавательно.Легко для понимания с иллюстрациями
и графики; определенно делает это
проще поглотить все
теорий. «
Victor Ocampo, P.Eng.
Альберта, Канада
«Хороший обзор принципов работы с полупроводниками. Мне понравилось пройти курс по
.мой собственный темп во время моего утро
до метро
на работу.»
Клиффорд Гринблатт, П.Е.
Мэриленд
«Просто найти интересные курсы, скачать документы и взять
викторина. Я бы очень рекомендовал
вам на любой PE, требующий
CE единиц. «
Марк Хардкасл, П.Е.
Миссури
«Очень хороший выбор тем из многих областей техники.»
Randall Dreiling, P.E.
Миссури
«Я заново узнал то, что забыл. Я также рад оказать финансовую помощь
по ваш промо-адрес электронной почты который
сниженная цена
на 40% «
Конрадо Казем, П.E.
Теннесси
«Отличный курс по разумной цене. Воспользуюсь вашими услугами в будущем».
Charles Fleischer, P.E.
Нью-Йорк
«Это был хороший тест и фактически подтвердил, что я прочитал профессиональную этику
коды и Нью-Мексико
правил. «
Брун Гильберт, П.E.
Калифорния
«Мне очень понравились занятия. Они стоили потраченного времени и усилий».
Дэвид Рейнольдс, P.E.
Канзас
«Очень доволен качеством тестовых документов. Буду использовать CEDengineerng
.при необходимости дополнительных
аттестат. «
Томас Каппеллин, П.E.
Иллинойс
«У меня истек срок действия курса, но вы все же выполнили свое обязательство и дали
мне то, за что я заплатил — много
оценено! «
Джефф Ханслик, P.E.
Оклахома
«CEDengineering предлагает удобные, экономичные и актуальные курсы»
для инженера »
Майк Зайдл, П.E.
Небраска
«Курс был по разумной цене, а материал был кратким и
в хорошем состоянии «
Glen Schwartz, P.E.
Нью-Джерси
«Вопросы подходили для уроков, а материал урока —
.хороший справочный материал
для деревянного дизайна »
Брайан Адамс, П.E.
Миннесота
«Отлично, я смог получить полезные рекомендации по простому телефонному звонку.»
Роберт Велнер, P.E.
Нью-Йорк
«У меня был большой опыт работы в прибрежном строительстве — проектирование
Строительство курс и
очень рекомендую .»
Денис Солано, P.E.
Флорида
«Очень понятный, хорошо организованный веб-сайт. Материалы курса этики Нью-Джерси были очень хорошими
хорошо подготовлены. «
Юджин Брэкбилл, P.E.
Коннектикут
«Очень хороший опыт. Мне нравится возможность загружать учебные материалы на
.обзор везде и
всякий раз, когда.»
Тим Чиддикс, P.E.
Колорадо
«Отлично! Сохраняю широкий выбор тем на выбор».
Уильям Бараттино, P.E.
Вирджиния
«Процесс прямой, без всякой ерунды. Хороший опыт».
Тайрон Бааш, П.E.
Иллинойс
«Вопросы на экзамене были зондирующими и продемонстрировали понимание
материала. Полная
, и комплексное ».
Майкл Тобин, P.E.
Аризона
«Это мой второй курс, и мне понравилось то, что мне предложили этот курс
поможет по телефону
работ.»
Рики Хефлин, П.Е.
Оклахома
«Очень быстро и легко ориентироваться. Я обязательно воспользуюсь этим сайтом снова».
Анджела Уотсон, П.Е.
Монтана
«Легко выполнить. Никакой путаницы при прохождении теста или записи сертификата».
Кеннет Пейдж, П.E.
Мэриленд
«Это был отличный источник информации о солнечном нагреве воды. Информативный
и отличное освежение ».
Luan Mane, P.E.
Conneticut
«Мне нравится подход к регистрации и возможность читать материалы в автономном режиме, а затем
вернитесь, чтобы пройти викторину «
Алекс Млсна, П.E.
Индиана
«Я оценил объем информации, предоставленной для класса. Я знаю
это вся информация, которую я могу
использование в реальных жизненных ситуациях »
Натали Дерингер, P.E.
Южная Дакота
«Обзорные материалы и образец теста были достаточно подробными, чтобы позволить мне
успешно завершено
курс.»
Ира Бродская, П.Е.
Нью-Джерси
«Веб-сайтом легко пользоваться, вы можете скачать материал для изучения, а потом вернуться
и пройдите викторину. Очень
удобный а на моем
собственный график «
Майкл Глэдд, P.E.
Грузия
«Спасибо за хорошие курсы на протяжении многих лет.»
Dennis Fundzak, P.E.
Огайо
«Очень легко зарегистрироваться, получить доступ к курсу, пройти тест и распечатать PDH
Сертификат. Спасибо за изготовление
процесс простой. »
Fred Schaejbe, P.E.
Висконсин
«Опыт положительный.Быстро нашел курс, который соответствовал моим потребностям, и закончил
один час PDH в
один час «
Стив Торкильдсон, P.E.
Южная Каролина
«Мне понравилось загружать документы для проверки содержания
и пригодность, до
имея для оплаты
материал .»
Ричард Вимеленберг, P.E.
Мэриленд
«Это хорошее напоминание об ЭЭ для инженеров, не занимающихся электричеством».
Дуглас Стаффорд, П.Е.
Техас
«Всегда есть возможности для улучшения, но я ничего не могу придумать в вашем
процесс, требующий
улучшение.»
Thomas Stalcup, P.E.
Арканзас
«Мне очень нравится удобство участия в викторине онлайн и получение сразу
Свидетельство. «
Марлен Делани, П.Е.
Иллинойс
«Учебные модули CEDengineering — это очень удобный способ доступа к информации по номеру
.многие различные технические зоны за пределами
по своей специализации без
надо ехать.»
Гектор Герреро, П.Е.
Грузия
Случайные переменные с согласованными по моментам функциями лестничной плотности
Appl Math Model. Авторская рукопись; доступно в PMC 2020 24 февраля.
Опубликован в окончательной отредактированной форме как:
PMCID: PMC7039250
NIHMSID: NIHMS1558465
Луис Г. Креспо
a Dynamic Systems and Controls Branch, NASA Хэмптон, Вирджиния 23681, США
Шон П.Kenny
a Dynamic Systems and Controls Branch, NASA Langley Research Center, Hampton, VA 23681, USA
Daniel P. Giesy
a Dynamic Systems and Controls Branch, NASA Langley Research Center, Hampton, VA 23681, США
Брет К. Стэнфорд
b Отделение аэроупругости, Исследовательский центр Лэнгли НАСА, Хэмптон, Вирджиния 23681, США
a Отделение динамических систем и средств управления, Исследовательский центр НАСА в Лэнгли, Хэмптон, Вирджиния 23681, США
b Отделение аэроупругости, NASA Langley Research Center, Hampton, VA 23681, USA
Abstract
В этой статье предлагается семейство случайных величин для моделирования неопределенности.Интересующие нас переменные имеют ограниченное опорное множество и заданные значения для первых четырех моментов. Мы представляем условия допустимости существования любой из таких переменных и предлагаем класс переменных, который соответствует таким ограничениям. Этот класс называется лестницей, потому что плотность его членов является кусочно-постоянной функцией. Выпуклая оптимизация используется для вычисления их распределений в соответствии с несколькими критериями оптимальности, включая максимальную энтропию и максимальное логарифмическое правдоподобие.Гибкость и эффективность лестниц позволяют моделировать явления, имеющие, возможно, перекос и / или многомодальный отклик при низких вычислительных затратах. Кроме того, мы предоставляем средства для учета неопределенности в распределении, вызванной оценкой лестниц по данным. Эти идеи иллюстрируются путем создания эмпирических моделей прогнозирования лестницы. Мы рассматриваем случай, в котором предсказатель точно соответствует моментам выборки (настройка, применимая к большим наборам данных), а также случай, когда предсказатель учитывает ошибку выборки в такие моменты (настройка, применимая к разреженным наборам данных).В качестве примера используется прогностическая модель динамики аэроупругого крылового профиля, подверженного флаттерной неустойчивости. Результирующий предсказатель не только точно описывает реакцию системы, но также позволяет проводить анализ рисков для безопасного полета.
1. Введение
Метамоделирование [1] — это процесс создания математической модели явления на основе заданных данных. Согласование прогнозов с наблюдениями путем корректировки гиперпараметров вычислительной модели — давний подход в байесовском выводе, оптимизации проектирования на основе надежности, алгоритмах согласования моментов и обратном распространении дисперсии [2–5].
В этой статье предлагается структура для характеристики одномерной случайной величины с учетом ограничений момента. Эти ограничения могут возникать из-за совпадения моментов выборки. В литературе доступно множество проблем моментов и приложений. Например, неравенства моментов используются для получения надежных оценок финансовых величин [6,7], баланса богатства и оптимизации портфеля [8]. В области науки принятия решений [9] границы моментов используются для динамического программирования, анализа решений с неполной информацией и байесовской статистики.
В частности, мы фокусируемся на переменных, имеющих конечное опорное множество и заданные значения для первых четырех моментов. Взаимозависимость требований, связанных с этим предписанием, определяет условия допустимости существования любой из таких переменных. Сначала мы изучаем это допустимое пространство, а затем выбираем конкретный класс переменных из, возможно, бесконечного множества, которые удовлетворяют ограничениям. Этот класс называется лестницей , потому что плотность его членов является кусочно-постоянной функцией на конечном наборе подинтервалов, разделяющих выбранный опорный набор.Лестницы позволяют описывать широкий спектр форм плотности, включая мультимодальные и / или сильно искаженные распределения. Однако, в отличие от стандартного спектра распределений, ступенчатая переменная не допускает алгебраического представления, а вместо этого определяется путем решения программы оптимизации.
Лестничные переменные могут быть сформированы в соответствии с одним из нескольких критериев оптимальности, включая максимальную энтропию, минимальный квадрат амплитуды, оптимальное соответствие цели и максимальное логарифмическое правдоподобие.Выпуклость обеспечивает существенные вычислительные преимущества, включая быстрое время вычислений и возможность решать проблемы с большим количеством проектных переменных и ограничений с использованием методов внутренней точки. Эта особенность делает их хорошо подходящими для многих практических приложений моделирования, требующих их многократных вычислений и моделирования, например, байесовской калибровки вычислительной модели, параметры которой представляют собой лестницы. Кроме того, мы разрабатываем метод, который позволяет учитывать ошибку выборки, которая возникает в результате оценки лестничного распределения на основе конечного набора наблюдений.В качестве примера используется моделирование и анализ рисков динамики аэроупругого профиля, подверженного флаттерной неустойчивости.
2. Предварительные сведения
Рассмотрим непрерывную случайную величину z с опорным набором Δ z = [ z min , z max ] и функцию плотности fz: Δz⊂ℝ → ℝ +. Обозначим m r r -й центральный момент z , который определяется как
mr = ∫Δz (z − μ) rfz (z) dz, r = 0,1,2,…
(1)
где μ — математическое ожидание z .Обратите внимание, что м 0 = 1, м 1 = 0, м 2 — дисперсия, м 3 — центральный момент третьего порядка и м 4 — центральный момент четвертого порядка. В этой статье, когда делается ссылка на момент r -й случайной величины, мы предполагаем, что соответствующий интеграл в (1) сходится для этого распределения.
Интересующие случайные переменные имеют ограниченный набор опор и заданные значения для μ , m 2 , m 3 и m 4 .Ограничение ограниченной опоры задается формулой Δ z ⊆ Ω z , где Ωz = [z_, z¯], с z¯≥z_. Моментные ограничения — это ограничения равенства в (1). Параметры этих ограничений будут сгруппированы в переменную θz∈ℝ6, заданную формулой
θz = [z_, z¯, μ, m2, m3, m4].
(2)
3. Выполнимость переменной, ограниченной
θНабор достаточных условий для допустимости случайной величины z , удовлетворяющей ограничениям, связанным с θ z , выведено из работы Шармы [10,11] и Кумара [12], определяется как 1 g ( θ z ) ≤ 0, где
g6 = m22 − m2 (μ − z_) 2 − m3 (μ − z_),
g7 = m3 (z¯ − μ) −m2 (z¯ − μ) 2 + m22,
g8 = 4m23 + m32 − m22 (z¯ − z_) 2,
g10 = −63m3− (z¯ − z_) 3,
g13 = (m4 − vm2 − um3) (v − m2) + (m3 − um2) 2,
для u = z¯ + z_ − 2μ и v = (μ − z _) (z¯ − μ).Условия выполнимости для переменных, поддерживаемых либо в Δz = ℝ, либо в Δz = ℝ +, имеющих моменты произвольного порядка, могут быть описаны как положительные полуопределенные ограничения [13,14]. Достаточные и необходимые условия выполнимости моментов с учетом конечного носителя, называемые проблемой моментов Хаусдорфа, задаются как набор бесконечного числа ограничений.
Допустимая область θ , Θ, определяется как
Θ = {θ: g (θ) ≤0}.
(3)
Можно показать, что множество невыпукло.показывает пересечения с некоторыми двумерными гиперплоскостями. Эти пересечения являются дополнением областей, выделенных синим цветом. Значение цветов будет объяснено в следующем разделе. Верхний левый, верхний правый и нижний левый участки соответствуют θ z = [−1, 1, μ , m 2 , 0.1, 0.2], θ z = [−1, 1, 0,1, м 2 , м 3 , 0.2] и θ z = [-1, 1, -0,2, 1/3, м 3 , м 4 ] соответственно. В этих трех случаях результирующие множества ограничены и имеют вершины на границах. Напротив, нижний правый график, который соответствует θz = [z_, z¯, 0,1,1 / 3, −0,15,0,2], дает неограниченное множество с гладкой границей.
Пересечение Θ с четырьмя двумерными гиперплоскостями (не синяя область) вместе с S (50) (желтая область) и S (100) (объединение областей желтого и оранжевого цветов).
4. Лестничные случайные величины
Может существовать бесконечно много случайных величин, реализующих точку в. Обратите внимание, что большинство стандартных семейств случайных величин могут реализовывать только подмножества меньшей размерности в Θ; Например, бета-случайная величина с четырьмя гиперпараметрами может представлять только точки, попадающие в точку пересечения Θ с 4-мерным многообразием. Семейства с шестью или более гиперпараметрами часто вносят ложные взаимозависимости между компонентами θ , которые они могут реализовать. = argminh {J (h): ∫z_z¯zfz (h) (z) dz = μ, ∫z_z¯ (z − μ) rfz (h) (z) dz = mr, r = 0,2 , 3,4},
(4)
где J — произвольная функция стоимости.Для простоты презентации мы отложим выбор J до следующего абзаца в этом разделе. Оптимизация в (4) невозможна для большинства стандартных семейств случайных величин по большей части Θ.
Сначала представлена концепция лестничной функции (или ступенчатой функции). Учитывая разбиение действительных чисел на конечное число интервалов, лестничная функция на этом разбиении является функцией, которая постоянна на каждом интервале. Использование этих функций нечувствительно к значению, которое функция принимает в конечной точке, разделяемой двумя соседними интервалами, поэтому мы не будем работать с этой точкой.Мы фокусируем наше внимание на семействе случайных величин, имеющих ступенчатую плотность, которые в дальнейшем будем называть ступенчатыми переменными. Кроме того, если мы ищем лестничную переменную, которая реализует параметры в θ z , мы сначала выбираем положительное целое число n b как количество интервалов в разделе. Затем мы потребуем, чтобы интервал [z_, z¯] был разбит на n b подинтервалов равной длины κ = (z¯ − z _) / nb точками разделения zi = z _ + (i − 1 ) κ для 1 ≤ i ≤ n b + 1.Тогда высота лестницы определяется выражением l∈ℝnb, где ℓ ≥ 0 и κ∑i = 1nbli = 1. потом
fz (h) (z) = {li∀z∈ (zi, zi + 1] для 1≤i≤nb, 0 в противном случае.
(5)
Затем мы применяем уравнение (4) к переменной лестницы В этой настройке гиперпараметр принимает вид h = [ θ z , n b ], где θ z ∈ Θ. Результирующая переменная лестницы, будет обозначаться как
имеет функцию плотности, предписанную формулой.= argminl≥0 {J (l): A (θ, nb) l = b (θ), θ∈Θ}.
(8)
где A∈ℝ5 × nb и b∈ℝ5 задаются формулами
A = [κeκcκc2 + κ3 / 12κc3 + κ3c / 4κc4 + κ3c2 / 2 + κ5 / 80],
(9)
b = [1μμ2 + m2m3 + 3μm2 + μ3m4 + 4m2000 + 6m
(10)
где c∈ℝnb — центры бинов, c i = ( z i + z i +1 ) / 2 с 1 ≤ i ≤ n b , c n — покомпонентная n -я степень от c , а e∈ℝnb — вектор единиц.
Далее изучаются несколько функций стоимости J in z ~ S z ( θ z , n b , J ). Первая стоимость, которую мы рассматриваем, это
Дж (л) = — E (л) ≔κ log (л) ⊤l,
(11)
где E — дифференциальная энтропия. Принцип максимальной энтропии гласит, что распределение вероятностей, которое лучше всего представляет текущее состояние знаний с учетом некоторой априорной информации, имеет наибольшую энтропию.Другими словами, следует выбрать такое распределение, которое оставляет вам наибольшую оставшуюся неопределенность / энтропию информации, которая согласуется с ограничениями. Таким образом, в расчеты не вносятся никакие дополнительные предположения или ошибки. В контексте лестничных переменных априорной информацией является набор ограничений, связанных с θ z . Следовательно, решение (8) для функции стоимости в (11) дает ступенчатую случайную величину максимальной энтропии.
Еще один класс функций стоимости:
Дж (l) = H (l, Q, f) ≔l⊤Ql + f⊤l,
(12)
где Q∈ℝnb × nb — положительная полуопределенная матрица, а f∈ℝnb. Эта структура превращает (7) в квадратичную программу. Например, используя J = H ( ℓ , I , 0) в (7), где I — единичная матрица, дает ступенчатую переменную, которая минимизирует квадрат суммы вероятностей на мусорные ведра. В качестве другого примера, если t∈ℝnb — это плотность целевой случайной величины при c , J = H ( ℓ , I , −2 t ), получаем ступенчатую переменную, которая минимизирует разность в квадрате между плотностями лестницы и мишени.Эта формулировка предоставляет средства для приведения переменной лестницы в соответствие с любой конкретной формой при соблюдении требуемых ограничений.
Другая функция стоимости — это (логарифм) вероятность данных в последовательности D = {z (j)} ,, для j = 1,… N . Когда наблюдения в последовательности независимы, мы имеем
Дж (l) = — L (l, D) ≔ − ω⊤ log (l),
(13)
где ω∈ℝnb задается формулой
ωi = ∑j = 1NI {z (j) ∈ [zi, zi + 1]},
а I — индикаторная функция.Лестничные переменные, основанные на (13), увеличивают вероятность данных. Лестницы максимального правдоподобия часто имеют PDF-файлы с большими перепадами между соседними ячейками. Способы сглаживания таких скачков приведены в Приложении.
Лестничные переменные с разными функциями стоимости для фиксированного гиперпараметра h показаны на. Компоненты θ представляют собой эмпирические оценки, полученные из ансамбля N = 1000 точек данных, взятых из механизма генерации данных (DGM) z = u 2 — v 3 , где u и v — стандартная униформа.На этом рисунке показана лестница с максимальной энтропией, лестница с минимальным квадратом правдоподобия и лестница, соответствующая целям, основанная на эмпирической плотности. Переменная максимальной энтропии демонстрирует наиболее плавное изменение плотности, тогда как соответствие цели лучше всего соответствует DGM. Шум в плотности согласования цели, вызванный шумом в эмпирической плотности, может быть устранен с помощью методов сглаживания ядра. Лестница, которая максимизирует вероятность получения данных, изучается в Приложении.
Лестничные плотности для максимальной энтропии (синий), минимального квадрата правдоподобия (красный) и соответствия цели (зеленый) для n b = 200.Плотность DGM показана черным цветом.
Лестницы, достигающие других критериев оптимальности, включая наибольшую / наименьшую вероятность данного события 2 , максимальное / минимальное значение данного квантиля и интервалы прогнозирования наибольшей / наименьшей ширины, могут быть легко сформулированы. Каждая из этих пар задач дает диапазон значений, в котором должна падать интересующая метрика для всех других лестничных переменных, ограниченных θ . Меньшие диапазоны получаются при наложении дополнительных ограничений, таких как симметрия, унимодальность, выпуклость или гладкость.Вычисляя диапазон всех возможных значений, мы устраняем субъективность, возникающую в результате предположения о конкретном распределении.
Когда J является выпуклой функцией, программа оптимизации в формуле. (8) выпукло, поэтому имеет единственный минимум. Выпуклость обеспечивает существенные вычислительные преимущества, включая быстрое время вычислений, способность эффективно решать проблемы с большим количеством проектных переменных и ограничений (порядка сотен тысяч) и гарантию того, что численный поиск сходится к глобальному минимуму.Кодируя допустимый набор (8) с помощью вычислительно управляемого самосогласованного барьера, методы внутренней точки гарантируют, что количество итераций, необходимых для схождения к оптимуму, ограничено полиномом по размерности и точности решения [17]. показывает зависимость процессорного времени, необходимого для вычисления лестничной переменной, от количества ячеек. Эти расчеты были выполнены на стандартном настольном компьютере с использованием имеющегося в продаже программного обеспечения. Назначение случайной величины влечет за собой установку иерархии из бесконечного числа моментов.В случае лестниц первые четыре момента задаются ограничениями, тогда как все остальные моменты задаются функцией стоимости. Следовательно, изменения в J могут отображать переменные со значительно отличающимися моментами более высокого порядка, таким образом, формами.
Время ЦП в зависимости от количества бункеров.
Доступны различные подходы к оценке плотности, включая ядерную оценку плотности [18] и ряд методов кластеризации данных [19]. Однако, в отличие от этих подходов, лестницы не стремятся представить плотность как комбинацию функций ядра.Это устраняет сложности, возникающие в результате предположения о неподходящей основе, практики, которая часто приводит к плохо обусловленным программам оптимизации, плотностям с ложными шаблонами и вероятностным хвостам, выходящим за пределы намеченного диапазона, например, представляя однородную переменную как смесь гауссиан. Вместо этого предлагаемая формулировка ищет крайние элементы ячейки вероятности согласования моментов с использованием выпуклой оптимизации. Лестничные переменные максимальной энтропии хорошо подходят для наборов данных небольшого размера, тогда как лестничные переменные максимального (логарифмического) правдоподобия лучше подходят для наборов данных среднего и большого размера.Это результат того, что эмпирические моменты сходятся к своим истинным значениям быстрее, чем лестничная плотность сходится к истинной плотности. Плотность переменных максимального правдоподобия, соответствующих различным наборам данных, имеющих одинаковое небольшое количество наблюдений, будет значительно различаться. В этом случае случайность выборки, а не лежащее в основе распределение DGM, формирует результирующую переменную. Это наблюдение применимо ко всем переменным максимального правдоподобия независимо от их структуры, т.е.э., подъезд или нет.
5. Выполнимость лестницы
Предполагаемое значение для n b может сделать (8) недопустимым. Этот раздел формализует это понятие. Возможная область лестничной клетки определяется как 3
S (nb) = {θ∈Θ: ∃l≥0 | A (θ, nb) l = b (θ)}.
Следовательно, набор S (nb) состоит из всех реализаций θ , для которых существует ступенчатая переменная, имеющая n b интервалов.Сделаем несколько замечаний относительно возможности лестницы. Обратите внимание, что осуществимость θ не подразумевает выполнимость лестницы, то есть θ∉S (nb), даже если θ ∈ Θ. Далее отметим, что выбранная стоимость Дж не влияет на осуществимость.
Определение принадлежности θ к S (nb) требует оценки выполнимости A ( θ , n b ) ℓ = b ( 9017 ) для ℓ ≥ 0.в формуле. (8) и определение того, является ли сходящееся решение допустимым минимумом. Этот подход является вычислительно жизнеспособным благодаря выпуклости программы оптимизации.
Теперь мы вернемся к численному сравнению S с. Цвета в нем показывают пересечения S (50) (область желтого цвета) и S (100) (объединение областей желтого и оранжевого цветов) с двумерными плоскостями в четырехмерном евклидовом пространстве. Эти цифры были получены путем вычисления ступенчатой переменной, соответствующей соответствующему значению θ в каждой точке точной сетки, а затем оценки сходимости алгоритма оптимизации.Точки, где алгоритм сходится к допустимому оптимуму, являются членами S, тогда как точки, где алгоритм расходится, нет. Расширение S в результате увеличения n b окрашено в оранжевый цвет. Приращения n b быстро уменьшают смещение между Θ и S (nb). Это смещение происходит около границы во всех случаях. Это было видно во всех проведенных численных экспериментах. Обратите внимание, что геометрия области невозможности лестницы, попадающей в Θ (например,g., область красного цвета, соответствующая n b = 100), зависит от границы набора. Например, верхний левый график показывает, что увеличение n b только расширило набор переменных, которые возможны по лестнице над нелинейной границей. В то время как большая часть Θ также находится в S (100), это не относится к большинству стандартных семейств случайных величин, например, 4-параметрическая бета-версия с поддержкой Δ z может реализовывать только ограниченные комбинации μ , м 2 , м 3 и м 4 , а представимые значения момента зависят от значений, принимаемых другими моментами.На нижнем правом графике видно, что в обеих возможных лестницах есть отверстия и шипы, похожие на сосульки. Эти особенности, вызванные изменениями ширины интервалов в результате изменения Ω, исчезают, когда используется фиксированное количество интервалов на единицу длины, ρ , т. Е. Nb = ⌈ρ (z¯ − z_ ) ⌉. Средства для поиска переменной лестницы, которая близко приближается к невыполнимой лестнице h , доступны в [20].
6. Оценка лестницы
Предположим, что образцы z (1), …, z ( N ) нарисованы независимо от фиксированной, но в остальном неизвестной DGM.Этот раздел посвящен оценке гиперпараметра h = [ θ z , n b ] лестничной переменной S z заданных данных. Следует использовать мнение экспертов, чтобы прописать к опоре n b и границу Ω z . Тогда как Ω z должно 4 содержать Δ˙ = [min {z (j)}, max {z (j)}], моменты μ , м 2 , м 3 и м 4 могут быть выбраны в качестве моментов выборки μ˙, мÀ2, мÀ3 и мÀ4.= 1 − elog (β) / (N − 1),
(15)
и β — параметр достоверности. См. Доказательство в Приложении. Уравнение (14) является формально проверяемым, не имеющим распределения и неасимптотическим результатом, применимым к любой стационарной DGM. Теория оптимизации сценария утверждает, что уравнение. (14) выполняется с вероятностью больше 1 — β , где β можно сделать очень маленьким, так что он теряет какое-либо практическое значение. Эта вероятность является ключом к получению гарантированных результатов, не зависящих от DGM.При определении подходящей переменной лестницы, уравнение. (14) эквивалентно
где, q i — доля интервала ( z i , z i +1 ], выходящего за пределы Δ˙. Это ограничение обеспечивает соответствие переменной лестницы к (14)
Теперь мы сосредоточимся на ошибке, возникающей при использовании моментов выборки в θ . Эта ошибка, предписываемая соответствующими распределениями выборки, может быть количественно оценена с использованием методов бутстрэппинга или теории центрального предела.Этот последний подход приводит к нормальным выборочным распределениям:
м2 ~ Нм2 (м˙2, м˙4 − m˙22N),
м3 ~ Нм3 (м˙3, м˙6 − m˙32−6m˙4m˙2 + 9m˙23N),
m4 ~ Nm4 (m˙4, m˙8 − m˙42−8m˙5m˙3 + 16m˙2m˙32N),
условно от θ ∈ Θ, где m˙k — момент отсчета порядка k . Эти выражения соответствуют произвольно распределенной переменной z для достаточно большого значения N [22]. Для небольших значений N методы начальной загрузки часто дают более точное приближение.Чтобы учесть ошибку выборки при оценке лестничной переменной, ограничения согласования моментов в (8) заменены ограничениями полиномиального неравенства
где μ ( ℓ ) = r 2 ℓ , m 2 ( ℓ ) = r 3 ℓ — μ () 2 , м 3 ( ℓ ) = r 4 ℓ — μ ( ℓ ) 3 — 3 μ ( ℓ ) м ( ℓ ) м 2 ( ℓ ) и м 4 ( ℓ ) = r 5 ℓ — 4 μ ( ℓ ) м 3 ( ℓ ) — 6 μ ( ℓ ) 2 m 2 ( ℓ ) — μ ( ℓ ) 4 — моменты лестницы, r i — это вектор-строка i для A в (9), а границы момента соответствуют контуру 1- α интервалы достоверности выборочного распределения.Например, μ˙ − 1,96 м˙2 / N≤μ (l) ≤μ˙ + 1,96 м2 / N для 95% доверительного интервала. Обратите внимание, что ящик моментов, определяемый формулами (17) — (20), может не полностью содержаться в Θ.
Следовательно, влияние ошибки выборки учитывается путем решения для лестницы с учетом ограничений неравенства (14) и (17) — (20). Обратите внимание, однако, что результирующая переменная не будет учитывать способ, которым распределение выборки распределяет вероятность в пределах выбранного блока моментов. Это соображение можно учесть, используя стоимость
Дж (l) = — E (l) −log {L (l)},
(21)
где L = Nμ (l) Nm2 (l) Nm3 (l) Nm4 (l) — функция правдоподобия выборочного распределения для независимых моментов.
В заключение, лестничные переменные обеспечивают (i) способность представлять широкий диапазон форм плотности, (ii) способность представлять большую часть возможного пространства Θ, (iii) структуру для учета ошибки выборки, присутствующей во время их оценка на основе данных и (iv) низкие вычислительные затраты, необходимые для эффективного выполнения многих задач количественной оценки неопределенности. Эта стоимость относится как к вычислению функции плотности, так и к моделированию результирующей переменной лестницы.
7. Примеры
Лестничные переменные используются ниже для создания эмпирических моделей прогнозирования. С этой целью мы предполагаем, что N независимых и одинаково распределенных пар ввода-вывода получены из механизма генерации данных (DGM), и обозначим D = {x (i), y (i)}, i = 1,… N, соответствующая последовательность данных. Например, при модальном анализе гибкой конструкции вход x представляет собой частоту возбуждения, тогда как выходной сигнал y представляет собой соответствующую амплитуду отклика в конкретном местоположении датчика.Случайные изменения свойств материала, граничных условий и шума измерений делают вывод y случайным.
Интересующие нас модели называются Модель лестничного предсказателя (SPM), потому что они характеризуют выход для любого заданного входа как лестничную переменную. Представленные ниже SPM основаны на данных. Таким образом, они не требуют каких-либо предположений относительно способа распределения данных в D. SPM требуют задания зависимых от входа функций θ
θy (x) = [y_ (x), y¯ (x), μy (x), m2, y (x), m3, y (x), m4, y (x)],
(22 )
в диапазоне ввода X .Обратите внимание, что θ y ( x ) является функциональным расширением θ z в уравнении. (2). В приведенных ниже примерах используется методика задания целевых функций θ y ( x ) согласно D, предложенная в [23].
Пример 1: Проверка модели . В этом примере мы генерируем SPM для DGM, о котором мы знаем все. Как и в методе изготовленных решений, проверка модели выполняется путем сравнения полученных предсказаний модели с истинным моделируемым явлением.
С этой целью мы рассматриваем DGM, показанный в верхней части. Вероятность попадания между любой парой соседних строк — 0,01. Обратите внимание, что распределение, включая его поддержку, расположение и количество режимов, сильно зависит от входных данных. Последовательность данных 5 с N = 1000 наблюдений была взята из DGM. показывает функции, соответствующие DGM (сплошные линии) вместе с целевыми функциями θ y ( x ) (пунктирные линии), извлеченные из данных.Обратите внимание, что целевые функции достаточно хорошо аппроксимируют функции DGM, несмотря на использование только 1000 наблюдений.
DGM (вверху), SPM с согласованием момента максимальной энтропии (второй), SPM, ограничивающий момент максимальной энтропии (третий), и SPM с минимальным (21) моментом (внизу).
Δ z и моменты для DGM (сплошные линии) и цели (пунктирные линии).
Целевые функции θ y ( x ) затем были использованы для построения SPM с согласованием момента S y ( x ) ( θ y ( x ) , 500, E ).Энтропия этого предсказателя Ex [E] = — 0,3642. показывает этот SPM на втором подзаголовке. Эта цифра была получена путем вычисления лестничных переменных по единой сетке входных значений в X , их выборки и группировки точек, принадлежащих одной и той же процентильной линии. Моментные функции, достигаемые SPM, неотличимы от целей. Сравнение между DGM и SPM показывает отличное согласие, измеренное квадратом разницы между парами соответствующих процентилей.Обратите внимание, что SPM хорошо описывает бимодальную структуру DGM, реплицируя области, в которых вероятность сильно сконцентрирована, то есть области на верхнем и нижнем пределе опоры, где группируются многие процентильные линии. Кроме того, асимметрия вероятностной массы внутри набора опор соответствует тем же образцам, что и в DGM. Вся эта информация неявно встроена в θ y ( x ) . Сравнение этого SPM с альтернативными методами моделирования доступно в ссылке [23].
Затем мы оцениваем влияние ошибки выборки в предписании θ y ( x ) . Чтобы количественно оценить разреженность набора данных, мы определяем эквивалентное количество наблюдений, n e , как
где 0 ≤ w ≤ 1 — весовая функция, использованная в [23]. Ошибка выборки в моментных оценках будет количественно определена с использованием разработок Раздела 6 для N = n e ( x ).Для этой последовательности данных значение n e находится в диапазоне от 47,15 до 112. Это указывает на то, что набор данных разрежен. показывает 95% доверительные интервалы ошибки выборки для четырех функций моментов в виде заштрихованных областей. Обратите внимание, что интервальные функции значительно осциллируют, достигая наибольшего разброса около x = 0.
Моменты SPM с ограниченным моментом на основе (11) (сплошная линия), SPM с ограниченным моментом на основе (21) ( пунктирная линия) и соответствующие границы (заштрихованные области).
Затем мы вычисляем SPM с максимальной энтропией, моментные функции которого могут принимать любое значение в пределах этих интервальных функций. Следовательно, каждая ступенчатая переменная, составляющая SPM, будет максимизировать энтропию, удовлетворяя при этом ограничению распространения (14), наряду с ограничениями блока моментов (17–20). Мы будем называть этот предсказатель ограниченным моментом SPM . Моменты, достигаемые этим SPM, показаны сплошными линиями на рис. Первые три момента различаются внутри своих интервалов, тогда как четвертый момент остается на нижней границе.Ослабление ограничений согласования момента до ограничений, ограниченных моментом, увеличивает ожидаемую энтропию с Ex [E] = -0,3642 до Ex [E] = 0,7484. Результирующий SPM показан на третьем подзаголовке. Обратите внимание на то, что наиболее характерные черты случайного процесса, такие как пики на границах набора опор и узоры линий внутри него, потускнели. Кроме того, обратите внимание, что разрывы производной в функциях моментов приводят к разрывам производной в линиях процентилей при соответствующих входных значениях.Такие разрывы могут быть устранены с помощью сглаживания ядра [25] или с помощью другой функции стоимости.
Последний подход рассматривается далее. В частности, мы рассчитаем SPM с ограниченным моментом, имеющий функцию стоимости в формуле. (21). Используя эту стоимость, результирующие лестничные переменные учитывают способ, которым распределение выборки распределяет вероятность в пределах блока моментов. Моментные функции, соответствующие этому SPM, показаны пунктирными линиями в. В отличие от других SPM, ограниченных моментом, новые моменты имеют непрерывные производные в пределах X .Результирующий SPM, показанный внизу, показывает плавные линии процентилей. Это достигается за счет небольшого уменьшения энтропии с Ex [E] = 0,7484 до Ex [E] = 0,7300. По мере увеличения n e ширина доверительных интервалов уменьшается, и SPM с ограничением момента сходятся к SPM согласования момента. Когда значение n e достаточно велико, набор данных больше не будет разреженным, и аналитик может предпочесть использование сопоставления целей или лестницы максимального логарифмического правдоподобия.
Пример 2: Анализ флаттера . Далее мы исследуем устойчивость профиля со степенями свободы по тангажу и врезанию, подверженного нестационарным аэроупругим воздействиям [26]. Флаттер, нелинейный отклик, вызванный бифуркацией Хопфа в динамике системы, может возникнуть при увеличении скорости свободного потока. При этом энергия потока передается на аэродинамический профиль, вызывая самоподдерживающиеся колебания, которые потенциально могут привести к потере контроля и повреждению конструкции. Скорость воздушного потока, при которой это происходит, называемая скоростью флаттера, является сложной функцией инерционных, геометрических, материальных и аэродинамических свойств и, как известно, очень чувствительна к неопределенностям [27].Физическая модель, действующая как DGM, представлена в приложении. Эта модель, абстрактная версия гибкой трехмерной модели крыла с динамикой изгиба и кручения [26], обычно используется для анализа систем управления реальных самолетов с неподвижным крылом.
Динамический отклик на конкретную скорость воздушного потока x (т.е., вывод в контексте этой статьи). Неотрицательные значения y обозначают нестабильный ответ, тогда как отрицательные значения соответствуют стабильному ответу. Изменчивость параметров системы делает и случайным процессом. Мы не только хотим определить вероятность нестабильности как функцию скорости воздушного потока, P [ y ( x )> 0], но также то, как возникает нестабильность. Нестабильности, для которых y положительны, но не слишком велики (поэтому время для амплитуды реакции на удвоение достаточно велико), можно смягчить, используя систему управления полетом или уменьшив скорость, тогда как нестабильности, для которых y положительный, и большой размер может не восстановиться.
Как и в предыдущем примере, SPM будет использоваться для характеристики отклика системы на заданные данные. С этой целью последовательность данных D = {x (i), y (i)} для i = 1,… 14000 была получена путем моделирования модели в приложении A.3 6 . показывает данные. Обратите внимание, что диапазон и распределение данных сильно зависит от скорости воздушного потока x . Диапазон варьируется от практически нулевого спреда при низких значениях x до значительных спредов при высоких значениях x .Кроме того, обратите внимание, что переход от стабильности к нестабильности происходит в диапазоне x ∈ [1,93, 2,71], так что P [ y (1.93)> 0] = 0 и P [ y (2. 71)> 0] = 1.
Данные (×), привязанные к опорному набору (линии).
Последовательность данных затем использовалась для оценки целевых функций в уравнении. (22). показывает границы диапазона данных, тогда как показывает целевые моментные функции и соответствующие им интервалы ошибок выборки.Обратите внимание, что ошибка выборки незначительна, когда x <3, и становится больше, когда увеличивается x . Функция момента третьего порядка показывает, что асимметрия распределения значительно меняется, принимая нулевые, положительные и отрицательные значения. Поскольку плотности неопределенностей, предписывающих случайный отклик, симметричны, асимметрия отклика вызвана исключительно лежащей в основе динамикой. Затем цели использовались для расчета лестничного предсказателя согласования моментов.показывает двухпроцентильные кривые полученного SPM.
Целевые функции (пунктирные линии) и их диапазоны ошибок выборки (заштрихованные области).
2-процентили SPM S y ( x ) ( θ y ( x ) , 250, E ).
Обратите внимание, что эта модель точно отражает основные характеристики данных, включая диапазон, зависящий от ввода, и вариации асимметрии. Следует отметить, что большая изменчивость, наблюдаемая в отклике системы, вызвана небольшими параметрическими неопределенностями менее 5% (см. Приложение).
Для сравнения были сгенерированы модель гетероскедастического гауссовского процесса (GP) и модель гауссовой смеси (GM) на основе одной и той же последовательности данных D. Соответствующие 2-процентили показаны на. Обратите внимание, что модель GP не может описать практически детерминированный отклик около x = 0, и что прогноз в области, где происходит переход к нестабильности, то есть 2 < x <3, существенно отличается от данных. Что еще более важно, неспособность модели давать негауссовские ответы часто делает полученные прогнозы неприемлемыми.В контексте этого примера это подразумевает получение ложного прогноза вероятности нестабильности во всем входном диапазоне. Модель GM 7 справа обеспечивает лучшее представление данных. Количество компонентов модели, а также границы ковариационных матриц были настроены таким образом, чтобы предотвратить получение негладкого предиктора с плохо обусловленными ковариационными матрицами. Несмотря на то, что модель GM достаточно хорошо описывает данные, предсказанное распределение в x <2 имеет слишком большую дисперсию, и несколько ложных паттернов встречаются внутри распределения, например.g., см. паразитные колебания большинства процентилей около x = 4,6. Модели GM сталкиваются с проблемами при описании плотностей, изменяющихся почти линейно в зависимости от входных данных, плотностей с разрывами, например, однородной случайной величины и DGM в Примере 1, и плотностей с небольшими отклонениями. Для описания этих характеристик требуется большое количество компонентов с небольшими ковариационными матрицами, что делает предсказатель негладким, а соответствующую оптимизацию — плохо обусловленной. Сравнение моделей в данных и относительно данных показывает, что SPM — лучший выбор для моделирования.SPM не только описывает распределение данных более точно, чем две альтернативы, но также избегает значительного объема настройки, необходимой для них.
Гетероскедастическая модель GP (слева) и модель GM (справа).
Затем SPM будет использоваться для оценки вероятности нестабильности в зависимости от воздушной скорости, а также серьезности такой нестабильности, т. Е. Степени сложности, необходимой для возврата самолета в устойчивый режим. Чтобы формализовать это понятие, рассмотрим метрику
λ (x) ≔∫0y¯ (x) y (x) fy (x) (y) dy.
(23)
При λ = 0 вероятность нестабильности равна нулю. Когда λ> 0, доля нестабильных ответов вносит вклад в λ пропорционально значению y . Обратите внимание, что λ может быть непропорционально вероятности нестабильности; например, отклик с вероятностью нестабильности 0,1 и длинным верхним хвостом может достичь большего значения λ, чем отклик с вероятностью нестабильности, равной единице. показывает вероятность нестабильности P [ y > 0] и λ как функции воздушной скорости.Допустимый диапазон скоростей воздушного потока при нулевой вероятности нестабильности составляет x ∈ [0, 1.93]. Если набор ответов, для которых λ <0,1 считается безопасным / восстанавливаемым, допустимыми становятся воздушные скорости ниже x = 2,3. Обратите внимание, что вероятность нестабильности достигает 0,62 в этом диапазоне. Таким образом, диапазон скоростей воздушного потока расширен на 20% за счет увеличения допустимого значения λ от нуля, что соответствует нулевой вероятности нестабильности флаттера, до 0.1.
Показатели нестабильности как функция воздушной скорости.
Вышеупомянутый прогнозирующий алгоритм лестницы сыграл важную роль в точном определении безопасной дальности полета с учетом серьезности нестабильности.
8. Выводы
В этой статье предлагаются лестничные переменные согласования моментов для моделирования неопределенности. Эти переменные имеют ограниченное опорное множество и заданные значения для первых четырех моментов. Мы предлагаем структуру выпуклой оптимизации для расчета их распределений по одному из нескольких критериев оптимальности.Эти критерии включают максимальную энтропию, минимальный квадрат амплитуды, оптимальное соответствие цели и максимальное логарифмическое правдоподобие. Выпуклость обеспечивает существенные вычислительные преимущества, включая быстрое время вычислений и возможность решения практически гладких плотностей вероятностей с использованием методов внутренней точки. Эта особенность делает лестницы подходящими для многих практических приложений, требующих их многократного расчета и моделирования, например, байесовской калибровки вычислительной модели, параметрами которой являются лестницы.Кроме того, лестницы позволяют моделировать явления, имеющие возможный перекос и / или многомодальный отклик, изменяющийся в ограниченном диапазоне.
Моделирование случайного процесса, поддерживающий набор и распределение которого сильно зависит от входной переменной, как в обоих примерах в статье, часто является сложной задачей. Гауссовские модели процессов, наиболее широко используемый метод непараметрического метамоделирования, не могут точно описать многие явления из-за их внутренней структуры. Модели гауссовой смеси лучше подходят для моделирования сложных откликов.Однако они сталкиваются с проблемами, когда основная плотность изменяется (почти) линейно с вводом, когда она имеет разрывы или когда она имеет небольшие отклонения. Модели прогнозирующих лестниц не страдают такими недостатками и не требуют значительного объема настройки, требуемого такими моделями. Эта настройка требуется не только для задания структуры модели и ее параметров из множества доступных опций, но и для того, чтобы численный поиск оптимума невыпуклой программы не попал в локальный минимум.
Кроме того, мы предлагаем стратегию оценки плотности лестницы с учетом данных. Этот подход ищет лестницу, моменты которой могут принимать любое значение в пределах интервалов прогнозирования оценок момента. Эффективность и гибкость лестничных переменных демонстрируется путем создания эмпирических моделей прогнозирования для двух примеров приложений. Полученные в результате лестничные предикторы не только точно описывают сложные реакции основных явлений во всем входном диапазоне, но также играют важную роль в выполнении совместного анализа рисков и неопределенностей для безопасного полета.Дальнейшая работа будет сосредоточена на дальнейшем ограничении переменных лестницы, чтобы соображения унимодальности, симметрии, гладкости и связности могли быть реализованы в рамках структуры выпуклого программирования.
Приложение A
A1. Затухание скачка
Плотность лестничных переменных максимального правдоподобия может иметь большие скачки между соседними интервалами. Несмотря на то, что гибкость лестничной переменной позволяет достичь вероятностей, которые намного превышают те, которые достигаются переменными из других семейств, поэтому они лучше описывают данные, можно было бы уменьшить такие скачки.Этого можно достичь, дополнительно наложив (7) выпуклым ограничением
где ν > 0 обратно пропорционально желаемому уровню гладкости, а C∈ℝnb × nb удовлетворяет
C = [1−1−12−10−12−1⋱⋱⋱0−12−1−11] ≽0.
(25)
Ограничение в (24) ограничивает сумму квадратов разности правдоподобия в соседних ячейках. Вверху отображается переменная максимального правдоподобия, соответствующая N = 500 наблюдениям, полученным из DGM в.Плотности для DGM и максимальная энтропия накладываются друг на друга. Скачки являются результатом больших различий в количестве наблюдений, попадающих в соседние интервалы. Внизу показаны лестничные переменные, которые являются результатом решения (8) со стоимостью (13) и ограничением (24) для нескольких значений ν . Обратите внимание, что параметр ν управляет степенью гладкости результирующей плотности. Переменная максимального правдоподобия вверху получается, когда ν велико.
Неограниченные (вверху) и ограниченные лестницы максимального правдоподобия (внизу).
A2. Оценка вероятности
Доказательство уравнения (14) выглядит следующим образом. Самый узкий интервал, содержащий образцы, Δ˙, является решением выпуклой программы min a , b { b — a : a ≤ z ( j ) , b ≥ z ( j ) , j = 1,… N }.= argmaxϵ {ϵ: (1 − ϵ) N + Nϵ (1 − ϵ) N − 1≤β},
оптимальная формула. (15).
A3. Динамическая модель для анализа флаттера
Уравнения флаттера упруго установленного крылового профиля [26] имеют следующий вид:
[mmbxθmbxθI] [h¨θ¨] + [kh00kθ] [hθ] = [- Lb (a + 1/2) L + M],
(26)
где h — врезание, θ — тангаж, м, — масса профиля, I — момент инерции, b — полухорда профиля, k h — жесткость при врезании, k θ — жесткость по тангажу, L — аэродинамическая подъемная сила и M — аэродинамический момент тангажа.Безразмерные параметры a и e определяют эквивалентное расположение соединения погружной пружины и центра масс, соответственно, x θ = e — a .
Нестационарные аэродинамические нагрузки обычно моделируются как
L = CLαρUbC (k) (h˙ + Uθ + b (1/2 − a) θ˙) + πρb2 (h¨ + Uθ˙ − abθ¨),
(27)
M = −πρb3 ( h¨ / 2 + Uθ˙ + b (1/8 − a / 2) θ¨),
(28)
где C Lα — наклон подъемной силы относительно угла атаки, ρ — плотность потока, U — скорость потока, а C ( k ) — функция Теодорсена [ 29] записано в терминах приведенной частоты к .Нестационарные аэродинамические эффекты часто моделируются с помощью функции Теодорсена, которая представляет собой комплексную функцию пониженной частоты, предназначенную для учета как амплитудного затухания, так и фазового запаздывания нестационарных воздушных нагрузок. Эта функция делает динамику в уравнениях. (26) — (28) нелинейные. Для решения этого уравнения предполагается решение следующего вида:
где p определяется как p = g + k i , k — вышеупомянутая приведенная частота, и g — параметр демпфирования, а i — мнимая единица.Объединение (26) — (29) приводит к:
[(U2 / b2) Mp2 + K + qA (p)] x¯ = 0
(30)
где q = ρU 2 /2 — динамическое давление, M и K — структурные матрицы из (26), а остальные члены собраны в A , комплексная аэродинамическая матрица, которая является высоконелинейной функцией p как из-за производных по времени от h и θ , которые приводят к p и p 2 членов, но также из-за зависимости функции Теодорсена от мнимой части p .
Результирующее нелинейное уравнение собственных значений может быть решено путем выбора начального предположения для каждой пары собственных значений ( p, , (p, x¯)) и повторения до сходимости, процесса, широко известного как метод pk [30] . В качестве альтернативы уравнение. (30) можно преобразовать в более крупное линейное уравнение на собственные значения, используя приближение рациональной функции:
A (p) ≈A0 + A1p + A2p2 + ∑j = 3nAjpp + γj − 2
(31)
где γ j — корни аэродинамического запаздывания, помещенные на стратегически пониженную частоту k значений.Поскольку A является известной функцией k i , члены A j могут быть вычислены с помощью наименьших квадратов вдоль мнимой оси.
Ar (k i) + iAi (k i) ≈A0 + A1 k i − A2k2 + ∑j = 3nAjk ik i + γj − 2
(32)
Аэродинамические состояния x a обозначаются как:
Комбинация уравнений. (30), (31) и (33) приводят к модели линейного изменения параметров (LPV) в U :
(pS1 + S2) {xpxxa1 ⋮ xan} = 0,
(34)
куда
S1 = [I00 ⋯ 00U2b2M + qA20 ⋯ 000I ⋯ 0 ⋮⋮⋮ ⋱ ⋮ 000 ⋯ I],
S2 = [0 − I0 ⋯ 0K + qA0qA1qA3 ⋯ qAn + 20 − Iγ1I ⋯ 0 ⋮⋮⋮ ⋱ ⋮ 0 −I0 ⋯ γnI].
Такой подход называется приближением Роджера [31] или p-методом.
Эту модель можно записать в шести безразмерных величинах: a , e , μ = m / ( πρb 2 ), r = I / (mb2), σ = ω h / ω θ и C Lα , где собственные частоты определены как ωh = kh / m и ωθ = kθ / I.Номинальные значения для этих параметров: a = −0,2, e = −0,1, μ = 20, r = 0,42, σ = 0,4 и C Lα = 2 π . Кроме того, безразмерная скорость потока определяется как V = U / b / ω θ . При наличии модели LPV в (34) стабильность системы задается способом, которым соответствующие собственные значения изменяются в зависимости от V .В приведенном выше примере мы предполагаем, что x = V и y — это максимальная действительная часть собственных значений погружения, шага и запаздывания. Кроме того, предполагается, что реакция модели носит случайный характер, поскольку параметры a и e изменяются равномерно в пределах 5% от их номинального значения.
Сноски
1 Векторные неравенства выполняются покомпонентно.
2 Полуопределенная оптимизация может использоваться для вычисления жестких границ P [ a ≤ z ≤ b ], когда Δz = ℝ или Δz = ℝ + для произвольных распределений, имеющих моменты произвольного порядка [14 ].Разработки в [15,16] позволяют учитывать дополнительные структурные свойства, такие как симметрия, унимодальность, выпуклость и гладкость.
3 Последующие разработки применимы независимо от того, учитывается ли ограничение в (24) или нет. Однако для простоты изложения мы предполагаем последний случай.
4 Выборочные оценки будут обозначены верхним индексом.
5 Последовательность данных и числовая установка, использованные здесь, также использовались в примере ссылки [24].Дополнительные подробности можно найти там.
6 Создание реалистичной вычислительной модели DGM является предполагаемой настройкой приложения для предлагаемых методов. Основная причина этого заключается в том, что «реальные данные» часто очень дороги или их невозможно получить (например, прогнозирование характеристик конструкции в условиях невесомости). Изучение влияния неопределенности на прогнозы, полученные на основе вычислительных моделей, является предметом первостепенной важности при оценке их производительности, безопасности и надежности.
7 Эта модель была получена путем сначала характеризации совместной плотности входа и выхода, а затем вычисления условной плотности выхода для сетки входов. Эта модель была рассчитана с использованием алгоритма максимизации ожидания с 200 компонентами.
Ссылки
[1] Симпсон Т., Пеплински Дж., Кох П., Аллен Дж. Метамодели компьютерного инженерного проектирования: обзор и рекомендации, Eng. Вычислить 17 (1) (2001) 129–150. [Google Scholar] [2] Аллен М., Мауте К., Оптимизация проектирования аэроупругих конструкций на основе надежности, Struct.Многопрофильный. Оптим 27 (2004) 228–242. [Google Scholar] [3] Элдред М.С., Агарвал Х., Перес В., Войткевич С., Рено Дж., Исследование формулировок методов надежности в DAKOTA / UQ, Struct. Инфраструктура. Англ. Maint. Manag. Жизненный цикл Des. Выполнять 3 (3) (2007) 199–213. [Google Scholar] [4] Свайлер Л.П., Адамс Б., Элдред М., Калибровка модели в условиях неопределенности: согласование информации о распределении, в: Материалы конференции по междисциплинарному анализу и оптимизации AIAA / ISSMO, Виктория, Британская Колумбия, Канада, 2008 г.[Google Scholar] [5] МакЭндрю CC, Компактное моделирование: принципы, методы и приложения, Статистическое моделирование с использованием обратного распространения дисперсии, Springer, Нью-Йорк, 2010. [Google Scholar] [6] Берцимас Д., Попеску I. соотношение между ценами опционов и акций: подход к оптимизации, Опер. Res 50 (2) (2002) 358–374. [Google Scholar] [7] Гранди Б., Цены опционов и распределение доходности базовых активов, J. Finance 46 (3) (1991) 343–556. [Google Scholar] [8] Гауи Л.Е., Окс М., Оустри Ф., Наихудшая оценка стоимости под угрозой и надежная оптимизация портфеля: подход конического программирования, Опер.Res 51 (4) (2003) 358–374. [Google Scholar] [9] Смит Дж. Обобщенные неравенства Чебышева: теория и приложения в анализе решений, Опер. Res 43 (5) (1995) 358–374. [Google Scholar] [10] Шарма Р., Деви С., Капур Г., Барнетт Н. С., Краткое замечание о некоторых границах, связывающих моменты нижнего порядка для случайных величин, определенных на конечном интервале, Int. J. Theor. Прил. Наука 1 (2) (2009) 83–85. [Google Scholar][11] Шарма Р., Кумар Р., Сайни Р., Капур, Дополнительные верхние границы для четвертого центрального момента с расширениями и приложениями, arXiv: 1503.03786 (2015).
[12] Кумар П. Моментные неравенства случайной величины, определенной на конечном интервале, J. Inequ. Pure Appl. Математика 3 (3, статья 41) (2002) 1–11. [Google Scholar] [13] Смит Дж. Моментные методы анализа решений, доктор философии. Диссертация, Стэнфордский университет (1990). [Google Scholar] [14] Берцимас Д., Попеску И., Оптимальные неравенства в теории вероятностей: подход выпуклой оптимизации, SIAM J. Optim 15 (3) (2005) 780–804. [Google Scholar] [15] Попеску I, Подход полуопределенного программирования к оптимальным оценкам моментов для выпуклых классов распределений, Матем.Опер. Res 30 (1) (2005) 1–23. [Google Scholar] [16] Тиан Р., Кокс С., Зулуага Л. Ф., Проблема моментов и ее приложения к оценке рисков, North Am. Актуарный J 21 (1) (2017) 242–266. [Google Scholar] [17] Немировски А.С., Тодд М.Дж., Приближенное истинное демпфирующее решение уравнения флаттера с помощью детерминантной итерации, Acta Numerica 1 (2008) 191–234. [Google Scholar] [18] Silverman BW, Оценка плотности для статистики и анализа данных, Chapman and Hall, 11 New Fetter Lane, London, England, 1986. [Google Scholar] [19] Fraley C, Raftery AE, Model-based clustering , дискриминантный анализ и оценка плотности, J.Являюсь. Стат. Assoc 97 (458) (2002) 611–631, DOI: 10.1198 / 016214502760047131. [CrossRef] [Google Scholar] [20] Креспо Л.Г., Гизи Д.П., Кенни С.П., О вычислении и формировании лестничных случайных величин, в: ESREL 2017, Порторож, Словения, 2017. [Google Scholar] [21] Campi MC, Гаратти С., Точная выполнимость рандомизированных решений неопределенных выпуклых программ, SIAM J. Optim 19 (3) (2008) 1211–1230. [Google Scholar] [22] Кендалл М., Стюарт А., Расширенная теория статистики, третье изд., Чарльз, Гриффин и Ко., Лондон, 1969. [Google Scholar] [23] Креспо Л.Г., Кенни С.П., Гизи Д.П., Прогностические модели лестниц для анализа надежности и рисков, Структурная безопасность. 75 (2018) 35–44. [Google Scholar] [24] Crespo LG, Giesy DP, Kenny SP, Случайные модели предикторов с непараметрической лестничной структурой, in: ESREL 2017, Portoroz, Slovenia, 2017. [Google Scholar] [25] Hastie T., Tibshirani R, Friedman Дж. Элементы статистического обучения, второе издание, Спрингер, Нью-Йорк, 2001. [Google Scholar] [26] Ходжес Д., Пирс А., Введение в структурную динамику и аэроупругость, Издательство Кембриджского университета, Нью-Йорк, 2002.[Google Scholar] [27] Беран П., Стэнфорд Б., Шрок С., Количественная оценка неопределенности аэроупругости, Ann. Rev. Fluid Mech (Жидкостный мех) 49 (1) (2017) 361–386. [Google Scholar] [28] Кампи М.К., Гаратти С., Подход с выборкой и отбрасыванием к оптимизации с ограничениями на случайность: осуществимость и оптимальность, J. Optim. Теория Appl. 148 (2) (2011) 257–280. [Google Scholar] [29] Теодорсен Т. Общая теория аэродинамической нестабильности и механизм флаттера, NACA, Нью-Йорк, 1949. отчет 496 [Google Scholar] [30] Хассиг Х. Приближенное истинное решение уравнения флаттера для демпфирования с помощью детерминантной итерации, Дж.Самолет 8 (11) (1971) 885–889. [Google Scholar] [31] Роджер К., Методы математического моделирования самолета для проектирования активного управления, Структурные аспекты активного управления, Центр технической информации обороны AGARD DTIC AD A 045242 CP-228, Нейи-Сюр-Сен, Франция: (1977) 4.1 –4.11. [Google Scholar]Площадь неправильных форм — формула, примеры, определение
Площадь неправильной формы означает пространство, занимаемое фигурой, которое измеряется в квадратных единицах. Неправильная форма может быть любого размера и длины.Неправильные формы можно увидеть повсюду вокруг нас, например, воздушный змей, ромбовидную фигуру, лист и т. Д. Любая форма, стороны и углы которой не равны по длине, называется неправильной формой.
Какова площадь неправильной формы?
Площадь неправильной формы — это размер области, покрытой этой формой. Неправильные формы — это те формы, которые не имеют равных сторон или равных углов. Чтобы найти область неправильной формы, ее можно разложить или разделить на несколько знакомых форм, а затем их площадь можно добавить, чтобы получить общую площадь.Мы можем видеть разные примеры неправильных форм в нашей повседневной жизни:
- Понаблюдайте за лестницей здания. Поверхность лестницы представляет собой неправильную форму, состоящую из многоугольников, таких как прямоугольники и квадраты.
- Детская площадка в школе с беговой дорожкой имеет неправильную форму, а также представляет собой сочетание правильных форм.
- Лист растения неправильной формы.
Единица площади неправильной формы выражается в м 2 , в см 2 , в 2 или в футах 2 .
Как найти область неправильной формы?
Чтобы найти область неправильной формы, мы должны знать, как разложить неправильную форму на знакомые формы.
Разобрать неправильную форму
Следующая форма представляет собой фигуру неправильной формы, площадь которой не может быть рассчитана по специальной формуле. Если мы разложим его на части, то увидим, что его можно разделить на многоугольники P, Q, R, S, T и U. Другими словами, эти многоугольники соединяются вместе, образуя неправильную форму.Итак, после разложения мы находим площадь этих многоугольников и складываем значения, чтобы получить площадь данной неправильной формы.
Возьмем другой пример. Данная фигура может быть разделена на несколько многоугольников A, B, C, D, E, F и G. Поскольку мы распознаем эти формы, мы можем легко найти их площадь и сложить их, чтобы получить площадь данной неправильной формы. .
Формула для определения площади неправильной формы
Нет прямой формулы для вычисления площади неправильной формы.В таких случаях мы используем разные методы для поиска местности.
Method 1: Как мы обсуждали ранее, чтобы найти площадь неправильной формы, мы можем разделить неправильную форму на знакомые многоугольники, а затем найти площадь каждого отдельного многоугольника.
Следовательно, площадь данной неправильной формы = Площадь всех многоугольников неправильной формы.
⇒ Площадь данной неправильной формы = площадь A + площадь B + площадь C + площадь D + площадь E + площадь F + площадь G
Метод 2: В некоторых случаях неправильная форма разделяется на небольшие квадраты или сетки.Общее количество единичных квадратов, попадающих в форму, определяет общую площадь. Следует отметить, что при вычислении площади для более точной оценки мы считаем квадрат «1», если заштрихованная область покрывает более половины каждого квадрата. Итак, в этом случае мы получаем примерный участок неправильной формы. Мы можем использовать этот метод для фигур, которые имеют кривые, подобные показанной на следующем рисунке.
Следовательно, площадь данной неправильной формы = Сумма всех единичных квадратов, попадающих под неправильную форму.
Часто задаваемые вопросы об областях неправильной формы
Какова площадь неправильной формы?
Площадь неправильной формы определяется как пространство, которое покрывает неправильная форма. Неправильные формы — это те формы, которые не имеют равных сторон или равных углов. Единица измерения площади неправильной формы выражается в квадратных единицах, например, м 2 , см 2 , в 2 или футы 2 .
Чем область неправильной формы отличается от области правильной формы?
Правильная форма имеет равные стороны и углы, а неправильная форма может быть любого размера и длины.Таким образом, площадь правильной формы может быть определена путем непосредственного применения для нее подходящих формул, тогда как площадь неправильной формы может быть найдена путем разложения неправильной формы на несколько правильных форм.
Есть ли формула для определения площади неправильной формы?
Не существует специальной формулы для определения площади неправильной формы, поскольку все стороны неправильной формы имеют разную длину. Иногда неправильная форма состоит из комбинации многоугольников, поэтому формула определяется путем разложения неправильной формы на правильные формы.
Как найти площадь неправильной формы?
Мы можем найти область неправильной формы, выполнив следующие шаги:
- Шаг 1. Разбейте неправильную форму на знакомые многоугольники.
- Шаг 2: Найдите сумму всех площадей известных многоугольников, чтобы найти площадь неправильной формы.
Как определить площадь неправильной формы с помощью метода единичных квадратов?
Мы можем найти площадь неправильной формы с помощью метода единичного квадрата, выполнив следующие шаги:
- Шаг 1: Разделите заданную неправильную форму на маленькие квадраты единичной квадратной площади.
- Шаг 2: Общее количество единичных квадратов, попадающих в форму, определяет общую площадь.
- Шаг 3: При вычислении площади для более точной оценки посчитайте квадрат как «1», если заштрихованная область покрывает более половины каждого квадрата.
Является ли метод единичных квадратов точным способом определения площади неправильной формы?
Нет, при измерении площади неправильной формы, если мы используем метод единичного квадрата, мы получаем приблизительное значение площади вместо точного значения.2+ 5x + 3`
Рисование парабол
Чтобы нарисовать график квадратного уравнения, выполните следующие действия:
(a) Проверить, является ли «a> 0» или «a <0», чтобы решить, является ли он U-образным или n-образным.
(б) Вершина: x — координата минимальной точки (или максимальной точки) равна
.`х = -b / (2a)`
(который можно показать, завершив квадратный метод, с которым мы встречались ранее).
Мы подставляем это значение x в нашу квадратичную функцию (выражение y ). Тогда у нас будут координаты ( x , y ) минимальной (или максимальной) точки. Это называется вершиной параболы.
(c) Координаты точки пересечения y (замените `x = 0`). Это всегда легко найти!
(d) Координаты точек перехвата x (подставьте `y = 0` и решите квадратное уравнение), если их легко найти.2− 8x + 6`
Ответ
Сначала мы идентифицируем, что `a = 2`,` b = -8` и `c = 6`.
Шаг (а)
Поскольку `a = 2`,` a> 0` следовательно, функция представляет собой параболу с точкой минимума и открывается вверх (П-образный)
Шаг (б)
Координата x минимальный балл:
`x = b / (2a) = (- (- 8)) / (2 (2)) = 8/4 = 2`
Значение точки минимума y равно
`y = 2 (2) ^ 2-8 (2) + 6 = -2`
Итак, минимальная точка — `(2, -2)`
Шаг (c)
Перехват y находится путем подстановки x = 0 в выражение y .2 -4x -3`, показывающая максимальную точку и пересечения с осями
Number Stairs Free Essay Example
Очерк, Страницы 7 (1512 слов)
Этот образец эссе на Number Stairs предоставляет всю необходимую базовую информацию по этому вопросу, включая наиболее распространенные аргументы «за и против». Ниже приведены вводная, основная и заключительная части этого эссе.
Часть 1: Для исследования взаимосвязи между общим значением лестницы и положением формы лестницы на сетке для других трехступенчатых лестниц. Число в нижнем левом углу фигуры лестницы обозначает ее положение. Цель этой части исследования — найти формулу для вычисления s-total (общего количества ступенек), зная s-число (количество ступенек).
Не теряйте время
Получите индивидуальное эссе на
«Число ступенек»
Получите качественную бумагупомогает студентам с 2016 года
45353625262725 + 26 + 27 + 35 + 36 + 45 = 194s-число = 25s-total = 1942111121231 + 2 + 3 + 11 + 12 + 21 = 50s-number = 1s-total = 502212132342 + 3 + 4 + 12 + 13 + 22 = 56s-число = 2s-total = 562313143453 + 4 + 5 + 13 + 14 + 23 = 62s-number = 3s-total = 622414154564 + 5 + 6 + 14 + 15 + 24 = 68s-number = 4s-total = 68 Еще одно наблюдение заключается в том, что в каждом столбце формы лестницы разница между этими строками чисел в одном столбце равна 10.(За исключением последнего столбца, который состоит только из 1 числа.) Разница между этими числами равна 10, потому что в сетке каждая строка содержит 10 чисел. Таблица результатов: s-numbers-total150 + 6256+ 632+ 646825194 Чтобы перейти от одного срок до следующего, просто добавляйте 6 каждый раз.
Однако это не показывает отношения между s-числом и s-итогом. Эта последовательность (добавление / вычитание числа каждый раз) известна как арифметическая последовательность. Формула для определения отношения между s-числом и s-итогом: первый член + общая разность x (n — 1).Первый член здесь 50, а общая разница составляет 6,50 + 6 (n — 1) = 50 + 6n — 6 = 6n + 442515165675 + 6 + 7 + 15 + 16 + 25 = 74 (6 x 5) + 44 = 74s-число = 5s-total = 742616176786 + 7 + 8 + 16 + 17 + 26 = 80 (6 x 6) + 44 = 80s-number = 6s-total = 8046363726272826 + 27 + 28 + 36 + 37 + 46 = 200 (6 x 26) + 44 = 200s-number = 26s-total = 200 После проверки формулы, чтобы увидеть, работает ли она, необходимо представить доказательство, чтобы показать, что она работает для любого s-числа (за некоторыми исключениями — см. «Заключение »).
Если s-число представлено как ‘n’: n Как упомянуто в цели, нижний левый угловой квадрат является s-числом (или в этом примере, известным как ‘n’nn + 1n + 2 Поскольку числа в сетка увеличивается на 1 каждый раз, я могу сказать, что два числа в одной строке увеличиваются на 1, таким образом диаграмма: «n + 1» и «n + 2».n + 20n + 10nn + 1n + 2 Как упоминалось ранее, числа в одном столбце имеют разность 10. Таким образом, «n + 10» и «n + 20», как показано на диаграмме. Затем я могу показать: (v) n + 20n + 10nn + 1n + 2 Если я сложу все эти значения (внутри квадратов) вместе: n + (n + 1) + (n + 2) + (n + 10) + ( n + 11) + (n + 20) = 6n + 44 * Доказательство 1: Обратите внимание, что в этом уравнении 6 n, потому что есть 6 квадратов. Таким образом, я доказал, что моя формула ‘6n + 44’ работает для каждого форма лестницы в этом размере сетки. Я могу продолжить это расследование, исследуя взаимосвязь между итоговыми значениями лестниц в других числовых сетках.Часть 2: Для дальнейшего изучения взаимосвязи между итоговыми значениями лестниц и другими ступеньками в других числовых сетках. Я решил исследовать взаимосвязь между итоговыми значениями лестниц в других числовых сетках, когда s-число остается постоянным, потому что будет легче наблюдать взаимосвязь между s-сеткой (сеткой номеров лестниц) и s-total. 7451231 + 2 + 3 + 4 + 5 + 7 = 22 сек = 3 сек = 229561231 + 2 + 3 + 5 + 6 + 9 = 26 сек = всего 4 сек = 2611671231 + 2 + 3 + 6 + 7 + 11 = 30 сек. -grid = 5s-total = 3013781231 + 2 + 3 + 7 + 8 + 13 = 34s-grid = 6s-total = 34 Таблица результатов: s-grids-total322 + 4436+ 4530 + 46341050 В таблице показано, что s- total увеличивается на 4 каждый раз, когда s-сетка увеличивается на 1.(Когда g = размер сетки), это потому, что: n + 2gn + gn + g + 1nn + 1n + 2; — Ранее я заметил, что разница между каждой строкой в одном столбце — это размер сетки. N + (n + 1) + (n + 2) + (n + g) + (n + g + 1) + (n + 2g) = 6n + 4g + (4) ** Примечание: 6n + 4g -> потому что есть 4g в формуле (как показано выше) .Теперь, когда я выяснил взаимосвязь между s-числом, s-сеткой и s-итогом, я могу продолжить это исследование, исследуя взаимосвязь между другими ступеньками, s -число, s-сетка и s-итоги.Я исследую взаимосвязь между s-числом, s-общим, s-сеткой и s-формой (формой лестницы). S-образная форма будет исследована путем увеличения; Увеличение длины на 1 квадрат и увеличение ширины на 1 квадрат. N Число s остается в нижнем левом углу формы лестницы. Вместо 6 квадратов их 10. Основываясь на моих предыдущих наблюдениях, я могу предсказать взаимосвязь между этой s-формой, s-числом, s-сеткой и s-итогом как: 10n + 10g + 10. проверьте мой прогноз: n + 3gn + 2gn + 2g + 1n + gn + g + 1n + g + 2nn + 1n + 2n + 3n + (n + 1) + (n + 2) + (n + 3) + (n + g) + (n + g + 1) + (n + g + 2) + (n + 2g) + (n + 2g + 1) + (n + 3g) = 10n + 10g + 10 Я должен исследовать следующую форму лестницы , который будет иметь высоту 5 квадратов и ширину 5 квадратов, всего 15 квадратов.n + 4gn + 3gn + 3g + 1n + 2gn + 2g + 1n + 2g + 2n + gn + g + 1n + g + 2n + g + 3nn + 1n + 2n + 3n + 4n + (n + 1) + (n + 2) + (n + 3) + (n + 4) + (n + g +) + (n + g + 1) + (n + g + 2) + (n + g + 3) + (n + 2g) + (n + 2g + a) + (n + 2g + 2) + (n + 3g) + (n + 3g + 1) + (n + 4g) = 15n + 20g + 20 Замечание: я заметил, что количество квадраты в каждой форме лестницы связаны с номерами треугольников. Например: последовательность чисел треугольника выглядит следующим образом: когда размер лестницы был равен 3, у нее было 6 квадратов. Когда размер формы лестницы был 4, у нее было 10 квадратов, а когда размер формы лестницы был 5, у нее было 15 квадратов.Как и на диаграмме на предыдущей странице, образец для размера формы лестницы такой же, как и для чисел треугольника. Это потому, что форма лестницы — треугольник: s-sizeno. из квадратов23 + 336+ 4410+ 5515+ 6621 Я могу предсказать количество квадратов, которые они есть для любого размера s, следуя последовательности чисел треугольника. Формула последовательности чисел треугольника: (где s — размер s). Я должен протестировать эту формулу, чтобы проверить, работает ли она. Я попробую его на s-size 7,7+ 6+ 5+ 4+ 3+ 2+ 1 Количество квадратов на этой диаграмме: 28 Поскольку я успешно проверил, что связь между s-размером и количеством квадратов в этой диаграмме s-size такой же, как у последовательности чисел треугольника; таким образом, формула для вычисления s-итога, когда известны s-число, s-сетка и s-размер, в настоящее время может быть вычислена как: s-total = (Примечание: X — неизвестное значение) В этом случае, Я использовал крестики дважды только потому, что они имеют одинаковую ценность.Поместив значение s-size и формулу в таблицу, я смог понять, почему я дважды использовал X в формуле. S-sizeformula36n + 4g + 4410n + 10g + 10515n + 20g + 20 Коэффициент имеет то же значение, что и Затем мне нужно было найти, как найти коэффициент и константу. Поскольку, похоже, нет постоянной разницы между коэффициентами, я буду использовать метод «изменение разностей», чтобы найти формулу для коэффициента. Существует формула для нахождения «изменяющейся разницы», известная как «Формула Грегори Ньютона».Во-первых, мне нужно было бы найти значение коэффициента, когда s-size равен 0. Очевидно, если s-size равен 0, s-total будет 0, так как нет квадратов для сложения его значения. . Чтобы показать, как я вычислил разницу, чтобы использовать «Формулу Грегори Ньютона», я составил таблицу различий: s-sizeX1st Difference2nd Difference3rd Difference4th Difference00 + 010+ 1+ 1+ 121+ 2+ 0+ 3+ 134+ 3 + 0+ 6+ 1410+ 4+ 10520После создания таблицы различий я смог выполнить «Формулу Грегори Ньютона» и выяснил, как найти «X»: Однако я должен проверить эту формулу, чтобы увидеть, работает ли она .Я протестирую его на s-size 6.n + 5gn + 4gn + 4g + 1n + 3gn + 3g + 1n + 3g + 2n + 2gn + 2g + 1n + 2g + 2n + 2g + 3n + gn + g. + 1n + g + 2n + g + 3n + g + 4nn + 1n + 2n + 3n + 4n + 5n + (n + 1) + (n + 2) + (n + 3) + (n + 4) + (n +5) + (n + g) + (n + g + 1) + (n + g + 2) + (n + g + 3) + (n + g + 4) + (n + 2g) + (n + 2g + 1) + (n + 2g + 2) + (n + 2g + 3) + (n + 3g) + (n + 3g + 1) + (n + 3g + 2) + (n + 4g) + (n + 4g + 1) + (n + 5g) = 21n + 35g + 35 Похоже, что этот раздел формулы работает. Теперь новая текущая формула: s-total = Важно: Однако у этой формулы есть свои ограничения. Например, ступенчатая лестница может быть помещена в определенную область, из-за которой ступенчатая лестница будет за решеткой.Это означает, что формула не может вычислить s-total, поскольку в таблице нет чисел. Возможно, можно найти еще одно ограничение, если он не может вычислять отрицательные числа. Я протестирую его на s-size 7, s-grid 8, а s-number будет 20.68606152535444454647363738394028232332021222324252620 + 21 + 22 + 23 + 24 + 25 + 26 + 28 + 29 + 30 + 31 + 32 + 33 + 36 + 37 + 38 + 39 + 40 + 44 + 45 + 46 + 47 + 52 + 53 + 54 + 60 + 61 + 68 = 1064 Теперь протестируем формулу. на отрицательные числа: 13141516171878
121234560-1-2-3-4-5-6-7-8-9-10-11-12-13-14-15-16-17 (-12) + (- 13) + ( -14) + (- 6) + (- 7) + (0) = -52 Похоже, что отрицательные числа не работают с этой формулой, поэтому формула ограничена положительными целыми числами и что форма лестницы не должна иметь какой-либо части он превышает сетку.Однако формула работает без ограничений. В заключение, соотношение между s-числом, s-сеткой, s-размером и s-общим является: s-total = (с некоторыми ограничениями, упомянутыми выше). Однако эту формулу можно упростить, поскольку, как упоминалось ранее, «Х» были в двух частях формулы, поэтому ее можно упростить. Первую часть уравнения, в которой находится формула для числа треугольника, также можно упростить до следующего: Расширение этого исследования может заключаться в исследовании взаимосвязи между отрицательными числами или трансформации формы лестницы. Не теряйте время
Получите индивидуальное эссе на
«Число ступенек»
Получите качественную бумагупомогает студентам с 2016 года
КАК РАССЧИТАТЬ ЛЕСТНИЦЫ, ПЕРИОД.
| Ваша основная лестница с прямым бегом. Плоские части являются «ступенями», а вертикальные части — «подступенками». |
Сначала выберите базовую конфигурацию лестницы — прямую, L-образную или U-образную. Если вы не мазохист, даже не думайте строить изогнутую лестницу. Правильный выбор зависит от того, сколько места у вас есть на плане этажа, от того, какой внешний вид вы хотите, и от нескольких других факторов, которые вам повезут.у нас нет места для обсуждения здесь.
После того, как вы выбрали прямую, L-образную или U-образную конфигурацию, определите общий подъем лестницы — расстояние по вертикали от одного этажа до другого. В этом примере предположим, что типичная высота составляет 106 дюймов.
| Традиционная U-образная лестница с полупустыней компактна и менее трудоемка для подъема. |
Хорошо. Допустим, мы хотим, чтобы наша лестница имела довольно пологий уклон, поэтому нам нужна высота подступенка где-то около 7 дюймов. Чтобы определить точную высоту, мы делим общий подъем от одного этажа к следующему — в нашем гипотетическом случае это 106 дюймов — на целые числа (представляющие общее количество подступенков), пока не получим цифру, максимально близкую к 7 дюймам, как возможный.
Путем проб и ошибок мы обнаружили, что деление общего прироста 106 ”на 15 дает около 7,07”. Это так близко, как если бы мы добрались до 7 дюймов, используя целое число, так что мы остановимся на этом. Это означает, что наша лестница будет иметь 15 подступенков по 7,07 дюйма каждая, что даст общий подъем 106 дюймов. Вперед — проверьте это на своем калькуляторе. Оно работает.
| Подъем, бег, общий подъем и общий пробег. Не ракетостроение. |
Теперь мы знаем как высоту нашей лестницы — 7,07 дюйма, так и ступеньку — 10 дюймов. На прямой лестнице все, что остается, — это найти общий пролет или длину лестницы. Для этого мы умножаем ширину ступени на общее количество ступеней, чтобы найти общую длину, необходимую для нашей лестницы. Вот в чем загвоздка: всегда на одну ступень меньше, чем количество подступенков, поскольку верхняя ступенька формируется самим верхним этажом.Итак, в нашем примере общий пролет лестницы будет: 10 дюймов проступей x (15-1) подступенков = 140 дюймов или 11-8 дюймов.
| Подступенки внешней лестницы не должны превышать шести дюймов, а ступени должны иметь глубину не менее двенадцати дюймов. Более пологий склон. тем лучше |
Помните, что общий подъем всегда делится на целое число, представляющее количество подступенков. Вы не можете начать с произвольного выбора высоты подступенка, потому что, когда вы подниметесь на верхнюю ступеньку лестницы, вы получите сиротскую ступеньку, которая ниже остальных. Также обратите внимание, что это работает для любого количества подступенков, включая ступеньки палубы, у которых между посадками всего несколько подступенков.Однако для любых наружных ступенек подступенок должен быть не выше 6 дюймов, а ступени должны быть не менее 11 дюймов в глубину.

 Не забывайте, что по такой лестнице не только нужно будет ходить по одному человеку, но иногда переносить мебель и крупногабаритные предметы, которые попросту не поместятся в узкий проем.
Не забывайте, что по такой лестнице не только нужно будет ходить по одному человеку, но иногда переносить мебель и крупногабаритные предметы, которые попросту не поместятся в узкий проем. Советуем количество ступенек сделать нечетным — таким образом, начинать и заканчивать подъем или спуск по лестнице вы будете одной и той же ногой.
Советуем количество ступенек сделать нечетным — таким образом, начинать и заканчивать подъем или спуск по лестнице вы будете одной и той же ногой. Простая арифметика.
Простая арифметика.
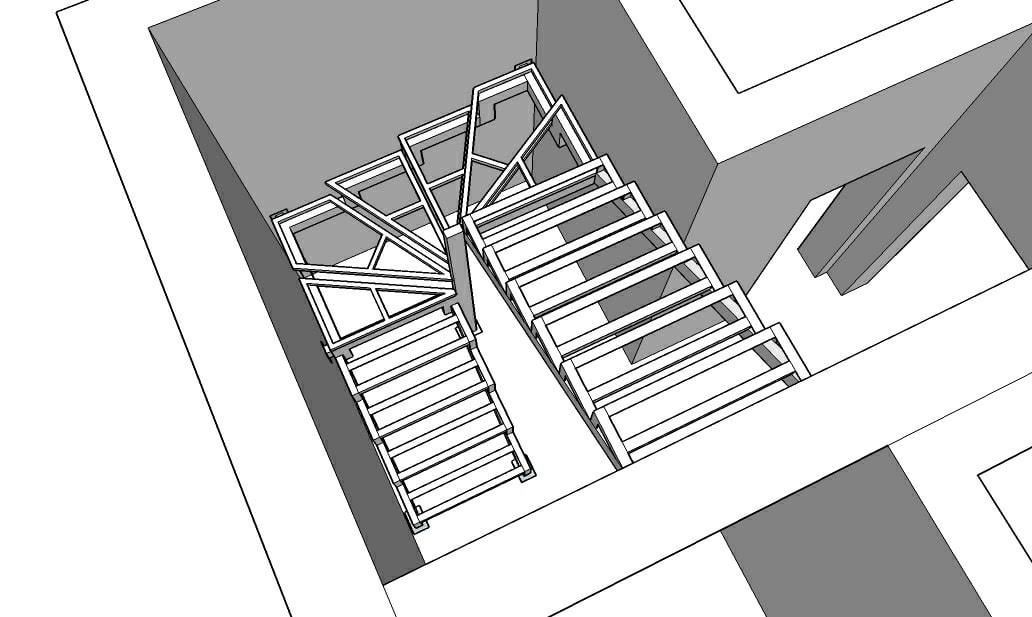 Она не только будет придавать комнате завершенный вид, и облагораживать помещение, но и прослужит не один десяток лет.
Она не только будет придавать комнате завершенный вид, и облагораживать помещение, но и прослужит не один десяток лет.

 Б. Безопасность жизнедеятельности (раздел «Охрана труда в строительстве»). Учебное пособие / Е.Б. Сугак. — М.: НИУ МГСУ, 2016. — 112 c.
Б. Безопасность жизнедеятельности (раздел «Охрана труда в строительстве»). Учебное пособие / Е.Б. Сугак. — М.: НИУ МГСУ, 2016. — 112 c. Плюсом подобных сооружений является их большая компактность по сравнению с площадочными конструкциями.
Плюсом подобных сооружений является их большая компактность по сравнению с площадочными конструкциями. Они могут быть установлены только в просторных частных домах или общественных сооружениях с высокими потолками. Кроме того, П-образные лестницы требуют довольно большого количества материала для своего сооружения, что может сильно отразиться на финансовой стороне вопроса.
Они могут быть установлены только в просторных частных домах или общественных сооружениях с высокими потолками. Кроме того, П-образные лестницы требуют довольно большого количества материала для своего сооружения, что может сильно отразиться на финансовой стороне вопроса.

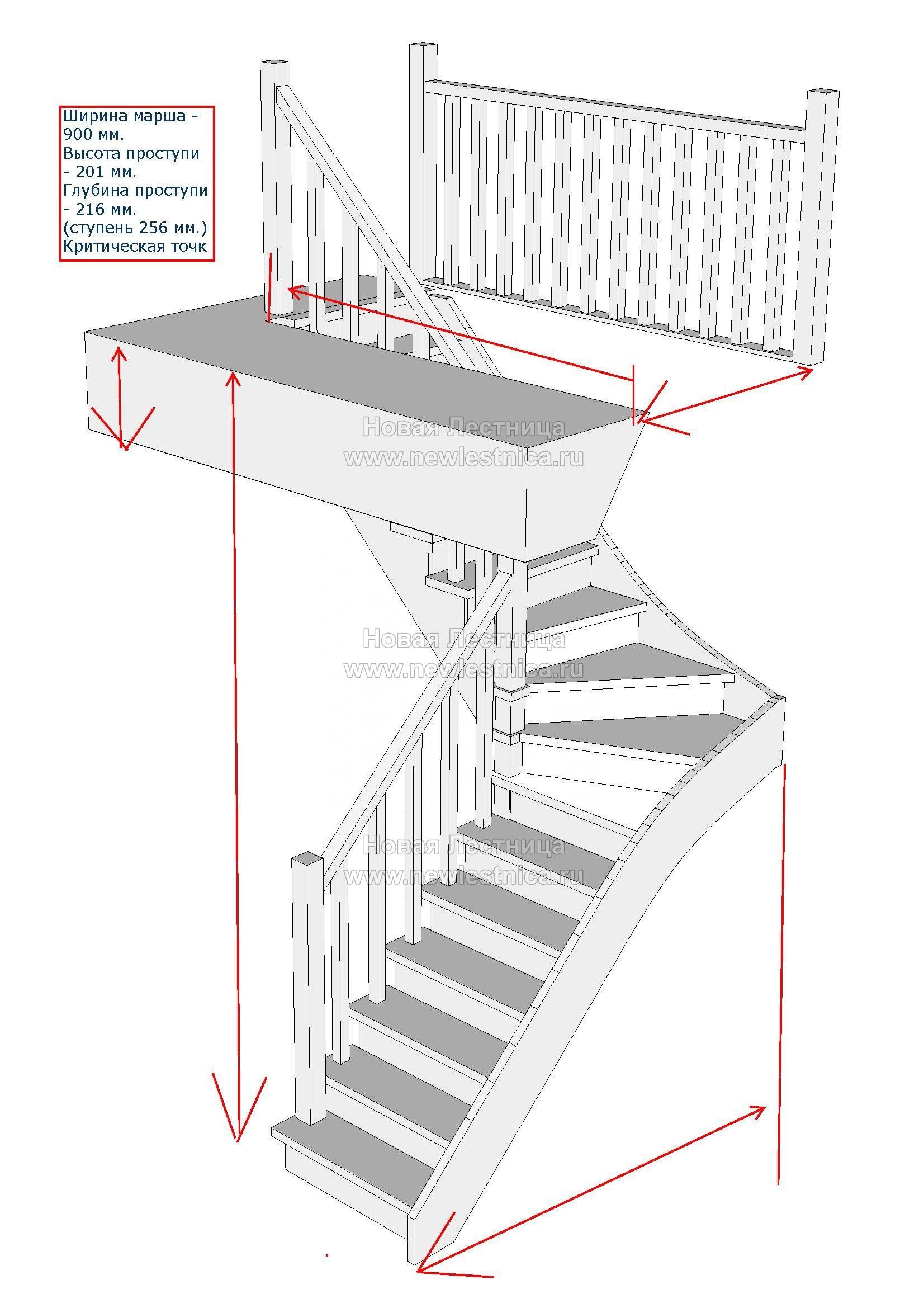 Поворотный марш нужно выделить на чертеже окружностью, разделить на одинаковые секторы, а затем перенести на проекцию. При этом необходимо учитывать все особенности данной схемы и наиболее подходящие величины.
Поворотный марш нужно выделить на чертеже окружностью, разделить на одинаковые секторы, а затем перенести на проекцию. При этом необходимо учитывать все особенности данной схемы и наиболее подходящие величины./35b5f5de97fe3bf.s.siteapi.org/img/a172768a8ed6b42672f37a436fd1df3a67975d50.jpg) Они являются довольно прочными, но в помещениях с высоким уровнем влажности лучше не устанавливать сооружения из подобного материала, или обрабатывать их специальными средствами от коррозии.
Они являются довольно прочными, но в помещениях с высоким уровнем влажности лучше не устанавливать сооружения из подобного материала, или обрабатывать их специальными средствами от коррозии. Часто в качестве каркаса лестницы используется металл, а ступени делаются из древесины.
Часто в качестве каркаса лестницы используется металл, а ступени делаются из древесины./35b5f5de97fe3bf.s.siteapi.org/img/838c80900aaa6c3d44a68297906298d60e2570b2.jpg)