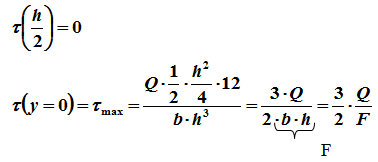Подбор сечения балки (сопромат)

Балка проверяется на прочность по наибольшим нормальным напряжениям, возникающие в поперечном сечении балки, где на эпюре 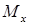 наибольший по абсолютному значению изгибающий момент. При поперечном изгибе в балке возникают и касательные напряжения, но они невелики, и при расчете на прочность учитываются только для двутавровых балок.
наибольший по абсолютному значению изгибающий момент. При поперечном изгибе в балке возникают и касательные напряжения, но они невелики, и при расчете на прочность учитываются только для двутавровых балок.
Условие прочности при изгибе по нормальным напряжениям: 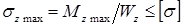 ,
,
где допускаемое напряжение 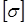 принимается, как и при растяжении (сжатии) стержня из такого же материала.
принимается, как и при растяжении (сжатии) стержня из такого же материала.
Формула условия прочности при изгибе по нормальным напряжениям позволяет осуществить подбор сечения балки при заданном материале и максимальном абсолютном значении изгибающего момента. Требуемый момент сопротивления балки при изгибе определяется из условия: 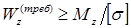 .
.
При изменении положения сечения по отношению к действующей нагрузке прочность балки существенно изменяется, хотя площадь сечения и остается неизменной. Например, для балки прямоугольного поперечного сечения с отношением сторон 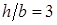 , расположенной таким образом, что высота прямоугольника h перпендикулярна нейтральной оси x, прочнее той же самой балки повернутой на
, расположенной таким образом, что высота прямоугольника h перпендикулярна нейтральной оси x, прочнее той же самой балки повернутой на 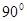 , в три раза, так как
, в три раза, так как 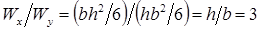 . В выражении для осевого момента сопротивления балки прямоугольного поперечного сечения при изгибе в квадрате стоит тот ее размер, который перпендикулярен нейтральной оси. Следовательно, сечение балки необходимо располагать таким образом, чтобы силовая плоскость совпадала с той из главных центральных осей, относительно которой момент инерции минимален ( ось, относительно которой главный момент инерции поперечного сечения максимален, является нейтральной осью). Это обстоятельство лишний раз подчеркивает важность темы «Определение положения главных центральных осей инерции поперечного сечения стержня».
. В выражении для осевого момента сопротивления балки прямоугольного поперечного сечения при изгибе в квадрате стоит тот ее размер, который перпендикулярен нейтральной оси. Следовательно, сечение балки необходимо располагать таким образом, чтобы силовая плоскость совпадала с той из главных центральных осей, относительно которой момент инерции минимален ( ось, относительно которой главный момент инерции поперечного сечения максимален, является нейтральной осью). Это обстоятельство лишний раз подчеркивает важность темы «Определение положения главных центральных осей инерции поперечного сечения стержня».
Проверка прочности двутавров
Для тонкостенных балок, например балок двутаврового профиля, проверка прочности производится следующим образом:
в наиболее удаленных от нейтральной оси точках прочность проверяется по формуле 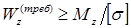 ;
;
в точках, где полка соединяется со стенкой прочность определяется по главным напряжениям.
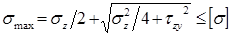
в точках, расположенных на нейтральной оси, прочность определяется по наибольшим касательным напряжениям:
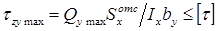
Балка. Виды и рациональные сечения балок
Балкой в механике называют брус, находящийся под действием изгибающих усилий, в частности, поперечных сил, моментов и распределенных нагрузок.
Деформацией балки является искривление ее продольной оси.
Кроме того, балкой называют элементы строительных и инженерных конструкций, воспринимающих преимущественно изгибающие нагрузки.
Как правило, они имеют прямолинейную продольную ось, а также постоянные размеры и форму поперечного сечения по всей длине.
В промышленности используются в основном металлические балки, обеспечивающие необходимую прочность, жесткость и устойчивость сооружений.
В строительстве помимо стальных также могут применяться железобетонные балки, усиленные стальной арматурой.
Виды балок
По способу закрепления и количеству опор балки делятся на:
а также на статически определимые и статически неопределимые.
Наш короткий видеоурок по расчету реакций опор балки:
Прочность и жесткость балок
На прочность и жесткость балки влияют:
- величина и положение внешних нагрузок;
- размеры, форма и расположение ее поперечного сечения;
- продольные размеры балки;
- материал;
- количество опор и способ закрепления в них.
Порядок расчета балок на прочность
Прочностные расчеты балок состоят из следующих этапов:
- При необходимости определяются опорные реакции;
- Строятся эпюры внутренних поперечных сил и изгибающих моментов;
- По эпюрам Q и M определяется опасное сечение балки.
Видео с расчетами и построениями эпюр для балки:
Далее для данного сечения может быть выполнен один из трех видов расчета:
Расчет балки на жесткость
При расчетах на жесткость рассчитываются прогибы в характерных сечениях балки, величина которых не должна превышать допустимых значений.
В случае если балка не удовлетворяет данному условию, необходимая жесткость достигается путем увеличения соответствующих размеров ее поперечного сечения.
Рациональные сечения балок
Наиболее предпочтительными сечениями балки являются двутавр и швеллер.
Они обеспечивают необходимую прочность балки, имея при этом наименьший собственный вес.
Это достигается за счет концентрации основной части металла в местах сечения, где возникают наибольшие нормальные напряжения.
Примеры расчетов балки >>
Построение эпюр >>
сечение балки — это… Что такое сечение балки?
kiriş kesiti
Турецко-русский словарь и русско-турецкий словарь по строительству и архитектуре. В.И. Макаров. 2005.
- сечение
- сечение колонны
Смотреть что такое «сечение балки» в других словарях:
Сечение нормальное — – сечение элемента плоскостью, перпендикулярной к его продольной оси. [СНиП 52 01 2003] Сечение нормальное – сечение, плоскость которого перпендикулярна продольной оси элемента [Полякова, Т.Ю. Автодорожные мосты: учебный англо… … Энциклопедия терминов, определений и пояснений строительных материалов
Сечение вынесенное — – сечение, расположенное на чертеже вне контура изображения предмета или в разрыве между частями одного вида. [ГОСТ2.305 2008] Рубрика термина: Проектирование Рубрики энциклопедии: Абразивное оборудование, Абразивы, Автодороги … Энциклопедия терминов, определений и пояснений строительных материалов
Сечение — – изображение фигуры, получающейся при мысленном рассечении предмета одной или несколькими плоскостями. На сечении показывается только то, что получается непосредственно в секущей плоскости. [ГОСТ 2.305 68] Рубрика термина: Общие термины… … Энциклопедия терминов, определений и пояснений строительных материалов
Опалубка, включаемая в расчетное сечение конструкции — – опалубка несъемная, включаемая в расчетное сечение конструкции. [ГОСТ Р 52086 2003] Рубрика термина: Опалубка Рубрики энциклопедии: Абразивное оборудование, Абразивы, Автодороги, Автотех … Энциклопедия терминов, определений и пояснений строительных материалов
Приведенное сечение — – железобетонное сечение, в котором арматура приведена к бетону с помощью коэффициента приведения. [Терминологический словарь по бетону и железобетону. ФГУП «НИЦ «Строительство» НИИЖБ им. А. А. Гвоздева, Москва, 2007 г. 110 стр.] Рубрика… … Энциклопедия терминов, определений и пояснений строительных материалов
Расчётное поперечное сечение — – уменьшенное поперечное сечение конструкции, используемое в расчете огнестойкости, получаемое путем удаления из поперечного сечения частей, обладающих нулевой прочностью и жесткостью. [EN 1992 1 2] Рубрика термина: Теория и расчет… … Энциклопедия терминов, определений и пояснений строительных материалов
Составное сечение сборно-монолитной железобетонной конструкции — (элемента конструкции) – поперечное сечение элемента конструкции, состоящей из заранее изготовленных (далее сборных) элементов и дополнительно уложенных на месте использования конструкции монолитного бетона и арматуры, объединенных для… … Энциклопедия терминов, определений и пояснений строительных материалов
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ — раздел механики твердого тела, изучающий напряжения и деформации, которые обусловлены силами, действующими на твердые тела элементы конструкции. Эту дисциплину можно характеризовать и как науку о методах расчета элементов конструкции на прочность … Энциклопедия Кольера
ПЛАСТИЧЕСКИЙ ШАРНИР — поперечное сечение балки или полосы, полностью находящейся в идеально пластич. состоянии. а Образование пластич. шарнира; б сечение балки в области пластич. шарнира А. Понятие «П. ш.» приобрело большое значение в связи с исследованием несущей… … Физическая энциклопедия
Книги
- Строим сами своими руками, Е. А. Гаврилова. Если вы мечтаете о собственном доме, но не знаете, как приступить к этому хлопотному делу, эта книга для вас. В ней вы найдете очень многое: этапы начального освоенияи планировки участка;… Подробнее Купить за 270 руб
Расчет прямоугольного сечения балки — Лекции и примеры решения задач технической механики
Задача
Для заданной стальной балки подобрать размеры прямоугольного поперечного сечения по условию прочности.
Соотношение сторон сечения h=2b (h – высота, b – ширина).
Полученные размеры принять согласно ГОСТ 6636.
Допустимые напряжения для материала балки [σ]=160МПа.
Решение
Предыдущие пункты решения задачи:
- Определение опорных реакций
- Построение эпюр внутренних поперечных сил и изгибающих моментов
- Расчет момента сопротивления сечения балки по условию прочности
Минимально необходимый расчетный момент сопротивления сечения балки составил
В случаях, когда система изгибающих нагрузок действующих на балку расположена в вертикальной плоскости сечение тоже следует располагать вертикально.
По справочнику находим формулу осевого момента сопротивления прямоугольного сечения
Используя заданное соотношение сторон (h=2b), уменьшим количество переменных в выражении
и запишем необходимое неравенство
Из заданного соотношения сторон определяем расчетную ширину сечения
Отметим, что полученные размеры являются минимально необходимыми для обеспечения прочности заданной балки.
При отсутствии дополнительных условий расчетные размеры можно округлить до целого значения в миллиметрах исключительно в большую сторону (h=153мм, b=77мм).
По ГОСТ 6636 нормальных линейных размеров выбираются ближайшие значения в сторону увеличения.
Следовательно, за окончательные размеры прямоугольного сечения балки принимаем: h=155мм, b=80мм.
После принятия размеров согласно ГОСТ заданное соотношение сторон может несколько измениться. Это нормально.
Оценка экономичности сечений >
Построение эпюры нормальных напряжений >
Другие примеры решения задач >
Рекомендуем:
- Скачать рамки А4 для учебных работ
- Учебные работы по всем предметам
- Скачать шрифты ГОСТ (чертежные)
- Миллиметровки А4 разного цвета
Расчет на прочность | ПроСопромат.ру
Задача 1
В некотором сечении балки прямоугольного сечения 20×30см М=28 кНм, Q=19 кН.
Требуется:
а) определить нормальное и касательное напряжения в заданной точке К, отстоящей от нейтральной оси на расстоянии 11 см,
б) проверить прочность деревянной балки, если [σ]=10 МПа, [τ]=3 МПа.

Решение
а) Для определения σ(К), τ(К) и maxσ,maxτ потребуется знать величины осевого момента инерции всего сечения IН.О., осевого момента сопротивления WН.О., статического момента отсечённой части и статического момента половины сечения Smax:

Тогда:

б) Проверка прочности:
— по условию прочности нормальных напряжений:

— по условию прочности касательных напряжений:

Задача 2
В некотором сечении балки М=10кНм, Q=40кН. Поперечное сечение – треугольное. Найти нормальное и касательное напряжения в точке, отстоящей от нейтральной оси на расстоянии 15 см.

 где
где 
Тогда
 где:
где:
 Тогда
Тогда

Задача 3
Подобрать сечение деревянной балки в двух вариантах: круглое и прямоугольное (при h/b=2), если [σ]=10 МПа, [τ]=3 МПа, и сравнить их по расходу материала.

Задаёмся направлениями опорных реакций А и В и составляем уравнения статики:
(1) ∑М(В) = F·8 – М – А·6 + (q·6)·3 =0,
откуда 
(2) ∑М(А) = F·2 – М + В·6 — (q·6)·3 =0,
откуда 
Iучасток

∑М(С) = М(z1) +F·z1=0,
ММ(z1) = —F·z1= — 30 ·z1 —
– уравнение прямой.
При z1 = 0: М = 0,
z1 = 2: М =- 60 кНм.
∑у= — F — Q(z1) = 0,
Q(z1) = — F = -30 кН – постоянная функция.
II участок


откуда
— уравнение параболы.
При z2=0: М = 0,
z2=3м: М = 30 · 3 – 5 · 32 = 90 — 45 = 45кНм,
z2=6м: М = 30 · 6 – 5 · 62 = 180 — 180 = 0.
∑у= Q(z2) — q·z2 + B= 0,
Q(z2) = q·z2 — B= 10·z2 – 30 – уравнение прямой,
при z2 = 0: Q = -30,
z2 = 6м: Q = 10·6 – 30 = 30.
Определение аналитического максимума изгибающего момента второго участка:
из условия находим
находим  :
:
 И тогда
И тогда

Заметим, что скачок в эп.М расположен там, где приложен сосредоточенный момент М = 60кНм и равен этому моменту, а скачок в эп.Q – под сосредоточенной силой А = 60 кН.
Подбор сечения балок производится из условия прочности по нормальным напряжениям, куда следует подставлять наибольший по абсолютной величине изгибающий момент из эпюры М.
В данном случае максимальный момент по модулю М = 60кНм
 откуда: :
откуда: :

а) сечение круглой формы d=?

б) сечение прямоугольной формы при h/b = 2:
 тогда
тогда

Размеры сечения, определенные из условия прочности по нормальным напряжениям, должны удовлетворять также условию прочности по касательным напряжениям:

Для простых форм сечений известны компактные выражения наибольшего касательного напряжения:
— для круглого сечения 
— для прямоугольного сечения 
Воспользуемся этими формулами. Тогда
— для балки круглого сечения при  :
:

— для балки прямоугольного сечения

Чтобы выяснить, какое сечение требует меньшего расхода материала, достаточно сравнить величины площадей поперечных сечений:
Апрямоугольного = 865,3см2 < Акруглого = 1218,6см2, следовательно, балка прямоугольного сечения в этом смысле выгоднее, чем круглого.
Задача 4
Подобрать двутавровое сечение стальной балки, если [σ]=160МПа, [τ]=80МПа.

Задаёмся направлениями опорных реакций А и В и составляем два уравнения статики для их определения:
(1) ∑М(А) = – М1– F ·2 — (q·8)·4 + М2 + В·6 =0,
откуда 
(2) ∑М(В) = – М1– А · 6 + F · 4 + (q·8)·2 + М2 =0,
откуда 
Проверка:
∑у = А – F – q · 8 + В = 104 – 80 – 20 · 8 +136 = 240 – 240 ≡ 0.

∑М(С) = М(z1) — М1=0,
М(z1) = М1= 40 кНм – постоянная функция.
∑у= — Q(z1) = 0,
Q(z1) = 0.
II участок
 — парабола.
— парабола.
Приz2=0: М = 40 кНм,
z2=1м: М = 40 + 104 – 10=134кНм,
z2=2м: М = 40+ 104 · 2 – 10 · 22 = 208 кНм.
∑у=А — q·z2 — Q(z2) = 0,
Q(z2) =А— q·z2 = 104 – 20·z2 – уравнение прямой,
при z2 = 0: Q = 104кН,
z2 = 6м: Q = 104 – 40 = 64кН.
III участок
 — парабола.
— парабола.
Приz3=0: М = 24+40=-16 кНм,
z3=2м: М = 24 + 136·2 — 10 (2+2)2 = 24 + 272 – 160 = 136кНм,
z3=4м: М = 24 + 136·4 – 10 (2+4)2 = 24 + 544 – 360 = 208 кНм.
∑у=В — q(2+z3 ) + Q(z3) = 0,
Q(z3) =- В + q(2+z3 ) = -136 + 20 (2+z3 ) – уравнение прямой,
при z3 = 0: Q = -136 + 40 = — 94кН,
z3 = 4м: Q = — 136 + 20 (2+4) = — 136 + 120 = — 16кН.
IV участок
 — парабола.
— парабола.
z4=0: М = 0кНм,
z4=1м: М = – 10кНм,
z4=2м: М = — 40кНм.
∑у=- q·z4 + Q(z4) = 0,
Q(z4) =q·z4 = 20·z4 – уравнение прямой.
Приz4 = 0: Q = 0,
z4 = 2м: Q = 40кН.
Проверяем скачки в эпюрах:
а) В эпюре М скачок на правой опоре величиной 24кНм (от 16 до 40) равен сосредоточенному моменту М2=24, приложенному в этом месте.
б) В эпюре Q три скачка:
первый из них на левой опоре соответствует сосредоточенной реакции А=104кН,
второй – под силой F=80кН и равен ей (64+16=80кН),
третий – на правой опоре и соответствует правой опорной реакции 136кН (94+40=136 кН)
Наконец, проектируем двутавровое сечение.
Подбор его размеров производится из условия прочности по нормальным напряжениям :

В сортаменте двутавровых профилей профиля с точно таким моментом сопротивления Wх нет. Есть № 40а с Wх=1190 см3 и № 45а с Wх=1430 см3
Попробуем меньший из них. Если принять двутавр № 40а, у которого Wх=1190 см3 , то наибольшее напряжение в опасном сечении будет:
 и перенапряжение составит
и перенапряжение составит что превышает рекомендуемую величину отклонения, равную 5%.
что превышает рекомендуемую величину отклонения, равную 5%.
Поэтому приходится принимать ближайший больший размер двутавра, а именно №45а, у которого Wх=1430 см3. В этом случае балка будет работать с недонапряжением:
 что меньше [σ]=160МПа на
что меньше [σ]=160МПа на 
Итак, принимается двутавр №45а, у которого: Wх=1430 см3, Iх=32240см4, Iх: Sх=38,6см, d=11,5мм.
Далее необходима проверка прочности по касательным напряжениям с помощью условия прочности :

Это условие прочности выполняется, даже с избыточным запасом.
Задача 5
Подобрать сечение балки, рассмотрев шесть вариантов форм и три вида материалов (древесина, чугун, сталь).
Решение

1.Определение опорных реакций
∑М(А) = F · 2 + М1 — М2— q·6·7 + В · 8 =0, ∑М(В) = F · 10 + М1— М2 – А · 8 + q·6·1 =0,
∑М(В) = F · 10 + М1— М2 – А · 8 + q·6·1 =0, Проверка:
Проверка:
∑у = – 20 – 40 ·6 +50+210 = — 260 + 260 ≡ 0.
2.Построение эпюр изгибающих моментов и поперечных сил.
I участок

∑М(С) = М(z1) + F·z1=0,
М(z1) = — F·z1= -20·z1.
При z1=0: М = 0,
z1=2м: М = – 40кНм,
∑у= — F— Q(z1) = 0,
Q(z1) = — 20кН.
II участок


z2=0: М = — 20 – 40 = -60 кНм,
z2=4м: М = 200 — 20 – 120 = 200 — 140 = 60кНм.
∑у=- F + А — Q(z2) = 0,
Q =- F + А= -20+50=30кН.
III участок
 — парабола.
— парабола.
Приz3=0: М = — 20·4= — 80 кНм,
z3=2м: М = 210·2 — 20·(2+2)2 = 420 – 320 = 100кНм,
z3=4м: М = 210·4 – 20 · (2+4)2 = 840 – 720 = 120кНм.
∑у= Q(z3) + В — q·(2+z3) = 0,
Q(z3) = — В + q·(2+z3) = — 210 + 40·(2+z3) – уравнение прямой.
Приz3 = 0: Q = -130кН,
z3 = 4м: Q = 30кН.
Q(z0) = — 210 + 40·(2+z0) = 0,
— 210 + 80 + 40·z0 = 0,
40·z0 = 130,
z0 =3,25м,

IV участок
 парабола.
парабола.
Приz4=0: М = 0 кНм,
z4=1м: М = – 20кНм,
z4=2м: М = — 80кНм.
∑у=- q·z4 + Q(z4) = 0,
Q(z4) =q·z4 = 40·z4 – уравнение прямой,
z4 = 0: Q = 0,
z4 = 2м: Q = 80кН.
3. Подбор сечений (опасное сечение по σ: |maxМ|=131,25кНм,
опасное сечение по τ: |maxQ|=130кН).
Вариант 1. Деревянное прямоугольное ([σ]=15МПа, [τ]=3МПа)

Принимаем: В=0,24м,
Н=0,48м.
Проверяем по τ:

Вариант 2. Деревянное круглое

Принимаем d=0,45м,
Проверяем по τ:

Вариант 3. Чугун : ([σР]=30МПа, [σс]=120МПа, [τ]=15МПа)

Принимаем b=0,19м, тогда h=0,38м, d=0,076м.
Проверка по τ:

b(у)= b — d= 0,19 — 0,076 = 0,114м

Вариант 4. Сталь, двутавр : ([σ]=160МПа, [τ]=80МПа).


по сортаменту Wх=953см3. Это №40: Ix=19062см4, Sх=545см3, d=0,83см.
Проверка по τ:

Вариант 5. Сталь, круглая труба 

Принимаем D=0,22м → d = 0,6·D =0,132м.
Проверка по τ:

Вариант 6. Сталь, прямоугольная труба 

b1= b — 2t = b — 2·0,1b = 0,8b,
h1= h — 2t = 0,8h,

Принимаем b=0,13м, h=0,26м.
Проверка по τ:

Кстати: какое из сечений стальной балки выгодней по расходу материала?
Двутавр — А = 72,6см2 = 72,6·10-4 = 0,00726м2,
круглая труба –
прямоугольная труба — 
Самый лёгкий: двутавр → самый выгодный с точки зрения изгиба.
10. Изгиб. Расчеты на прочность и жесткость при изгибе » СтудИзба
10. Изгиб. Расчеты на прочность и жесткость при изгибе
10.1 Чистый изгиб
Расчетные формулы для определения нормальных напряжений при изгибе обычно выводят из рассмотрения плоского чистого изгиба, который является наиболее простым случаем изгиба (рис.10.1).
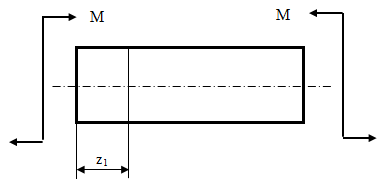
Рис. 10.1 Плоский чистый изгиб
Чистый изгиб – такой вид нагружения, при котором в поперечных сечениях бруса возникают только изгибающие моменты Мх, а Q=0.
Чистый изгиб характерен тем, что из шести компонентов внутренних усилий только изгибающий момент не равен 0, а поперечные и нормальные силы отсутствуют. Для тех участков стержня, где соблюдается это условие, изгибающий момент остается постоянным (М = const). Изгибающий момент численно равен сумме моментов всех внешних сил, действующих на отсеченную часть балки относительно оси Ох. Эпюра изгибающих моментов строится на сжатом волокне. При этом изгибающий момент в балках считается положительным, если сжаты верхние волокна, т. е. элемент изгибается выпуклостью вниз.
Рассмотрим три стороны задачи об изгибе:
1. Статическая сторона задачи:
Условия чистого изгиба могут возникать при различных внешних нагрузках. Характерный пример показан на рисунке (простейший двухопорный стержень, нагруженный силами Р) (рис. 10.2).

Рис. 10.2 Напряжения при чистом изгибе
Рассмотрим условие равновесия, связывающее напряжения и внутренние усилия в поперечном сечении балки (рис. 10.3), опуская индекс x y момента, получим
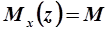 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)

Рис. 10.3 Поперечное сечение балки
2. Геометрическая сторона задачи:
При изгибе под действием моментов М ось балки искривляется (установлено экспериментально).

Рис. 10.4 Сетка, предварительно нанесенная на балку
Наблюдая за деформацией сетки, предварительно нанесенной на балку (рис. 10.4), можно заметить, что продольные линии при чистом изгибе искривляются по дуге окружности, контуры поперечных сечений остаются плоскими кривыми, пересекая продольные линии под прямыми углами (рис. 10.5). Это говорит о том, что при чистом изгибе поперечные сечения остаются плоскими и, поворачиваясь, становятся нормальными к изогнутой оси балки.
Фактически это есть доказательство того, что все сечения однородной балки при чистом изгибе не искривляются, а лишь поворачиваются. Это утверждение, будучи точным, для чистого изгиба, в общем случае является приближенным и именуется гипотезой плоских сечений (Бернулли).

Рис. 10.5 Деформация участка балки при чистом изгибе
Поворот плоских поперечных сечений одного относительно другого является результатом образования деформаций при чистом изгибе.
В сжатой области (сверху) волокна укорачиваются, а в зоне растяжения удлиняются. Зона растяжения в сечении балки разделяются нейтральным слоем с радиусом кривизны ρ. Длина нейтрального слоя при изгибе остается неизменной.
Рассмотрим два смежных сечения a и b, расположенных между собой на расстоянии dz (рис. 10.6).
Предположим, что левая часть неподвижна, а правая поворачивается относительно левого участка.





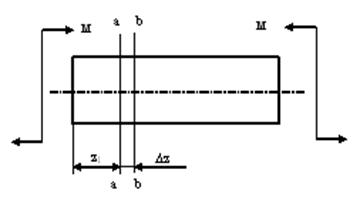
Рис. 10.6 Поворот правого участка относительно левого
При чистом изгибе найдем из рассмотрения деформации участка балки длиной dz относительное удлинение некоторого волокна, находящегося на расстоянии у от нейтрального слоя 
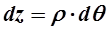
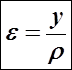 (5) —относительное удлинение участка
(5) —относительное удлинение участка
3. Физическая сторона задачи:
При чистом изгибе вводится предположение о ненадавливаемости продольных слоев (рис.10.7).
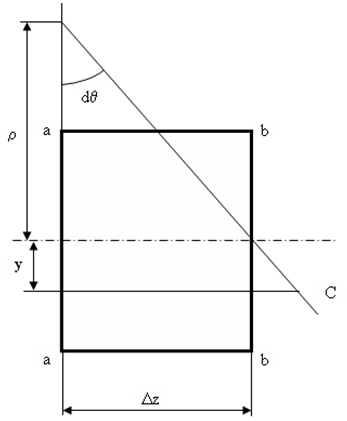
Рис. 10.7 Деформация участка балки длиной dz
t = 0 – касательное напряжение
s¹0 – нормальное напряжение
Так как t = 0, то это значит, что волокна балки находятся в линейно напряженном состоянии
 (6) — применяем закон Гука
(6) — применяем закон Гука
4. Объединяем три стороны задачи:
(5)®(6) Þ  (7)
(7)

(7)®(2)Þ 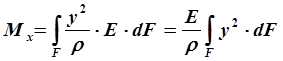

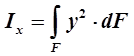 — осевой момент инерции, зависит от формы, размеров.
— осевой момент инерции, зависит от формы, размеров.
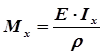
 (8), где Е∙Ix — жесткость сечения при изгибе
(8), где Е∙Ix — жесткость сечения при изгибе
Изменяется s по высоте сечения по линейному закону:

Напряжения при изгибе:
 (9) – нормальные напряжения при изгибе.
(9) – нормальные напряжения при изгибе.

Рис. 10.8 Сечение не имеющее горизонтальной оси симметрии
Максимальное напряжение при изгибе возникает в точках, наиболее удаленных от нейтральной линии.
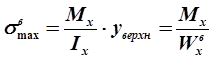
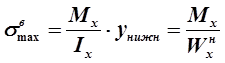
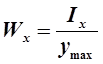 — осевой момент сопротивления сечения
— осевой момент сопротивления сечения
(9)®(4)Þ 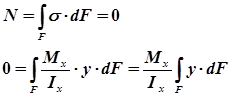
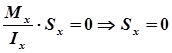 — статический момент инерции
— статический момент инерции
Значит, ось х – центральная. Таким образом, центр инерции проходит через центр тяжести сечения.

 — центробежный момент инерции
— центробежный момент инерции

Через ось у проходит силовая плоскость, значит, оси x и у – главные центральные оси.
Мы получили условия существования прямого изгиба (когда деформирование бруса происходит в силовой плоскости).
Для сечений с двойной симметрией унижн=уверхн=уmax
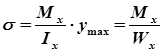 , где
, где 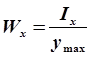
 — условие прочности при изгибе.
— условие прочности при изгибе.
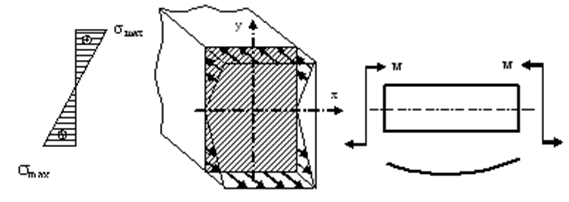
Рис. 10.9 Эпюра нормальных напряжений и сечение с горизонтальной осью симметрии
Пример (Рис. 10.10)
Подобрать номер двутавра

Рис. 10.10 Расчетная схема
Дано:
P=40 кН
A=1 м
[s]=160 МПа
Решение:
Растяжение – сжатие:
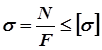
Кручение:

Изгиб:
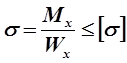
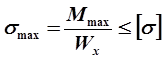 — условие «экономичности»
— условие «экономичности»
 ,
, 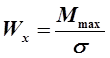
Строим эпюры Q и M (рис. 10.11)(эпюра М строится на сжатых волокнах)
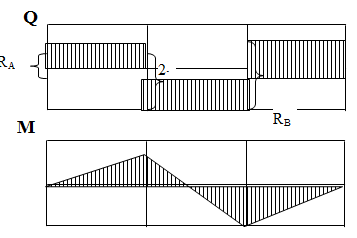
Рис. 10.11 Построение эпюр Q и M
Для этого определяем реакции RA,RB, используя уравнения равновесия
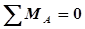 ,
, 
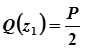 ,
,
 ,
,

 ,
,
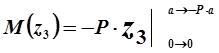
Опасное сечение над опорой В
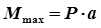
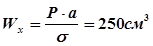
Двутавр №22, 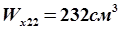
Для №22 перегрузка

Пример (И-1)
Для балки (Рис. 10.12) из расчета на прочность по нормальным напряжениям подобрать сечение в двух вариантах а) двутавровое б) полый прямоугольник. Проверить прочность балки по касательным напряжениям для двух вариантов. Построить эпюру касательных напряжений для прямоугольного сечения. Определить вертикальное перемещение сечения С. сравнить вес балок с прямоугольным и двутавровым сечением.
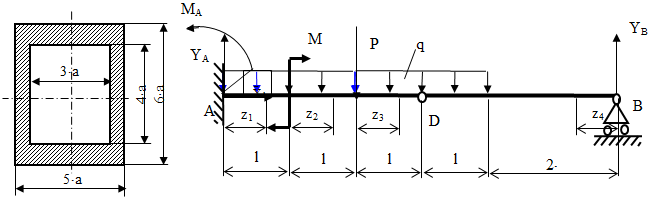
Рис. 10.12 Прямоугольное полое сечение и расчетная схема
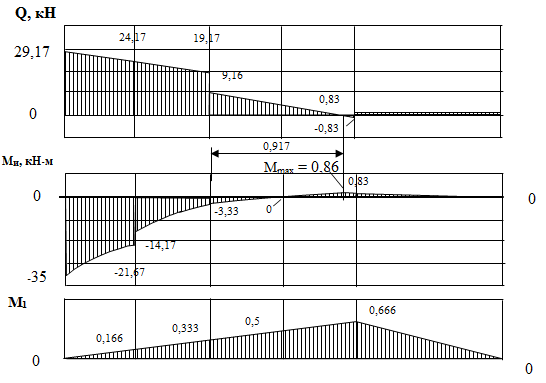
Рис.10.13 Построение эпюр Q и M
Дано:
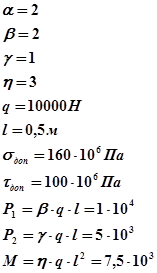
Решение:
Y: 
(у правой) 

(MD правой) 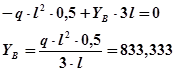

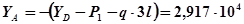


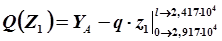
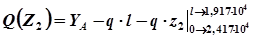
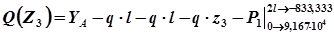
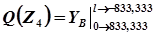
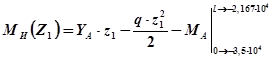

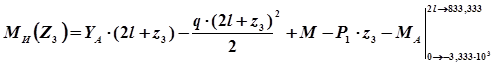
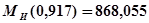
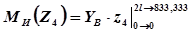
На третьем участке определяем максимум для момента:


Находим величину момента сопротивления:
1)для двутавра

подбираем номер двутавра №22 Wx.22=232·10-6

Проверка:  % (недонапряжение)
% (недонапряжение)
Подбираем номер двутавра №20а Wx.20а=203·10-6
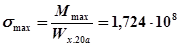
Проверка: 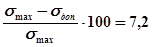 % (перенапряжение)
% (перенапряжение)
Т.к. на практике допускаются перенапряжения до 5 %,
то выбираем № 22
2)для специального сечения
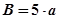



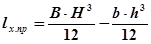

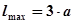


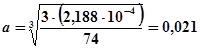 м
м
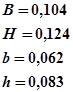
Определим площадь этого сечения:
 м2
м2
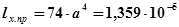
Проверим прочность балки по касательным напряжениям для двух вариантов сечений:
1)для двутавра
 м
м
 м
м

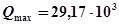
 Па (меньше τдоп)
Па (меньше τдоп)
Двутавр удовлетворяет требованиям прочности
2)для прямоугольника
τ1=0

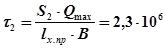 Па
Па
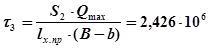 Па
Па

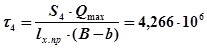 Па
Па
 Па
Па
Определим вертикальное перемещение в сечении с:

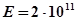 Па
Па
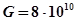 Па
Па
1-й участок

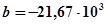


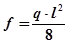
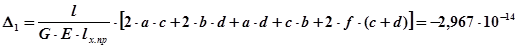
2-й участок
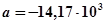



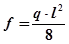
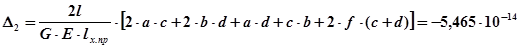
3-й участок
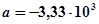
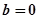
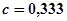
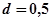
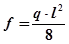
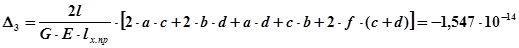
4-й участок

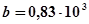
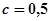

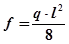
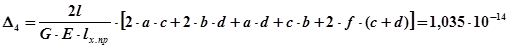
5-й участок
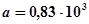
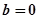
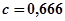

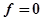
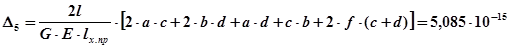
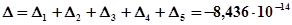
Определяем металлоемкость:
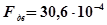

Таким образом, балка двутаврового сечения обладает меньшей металлоемкостью, чем балка в виде прямоугольника(рис.10.14 и рис.10.15).

Рис. 10.14 Эпюра касательных напряжений для прямоугольного сечения

Рис. 10.15 Двутаврное сечение балки
10.2 Поперечный изгиб
Поперечный изгиб – это такой вид нагружения, при котором в поперечных сечениях бруса возникают не только изгибающие моменты Мх, но и поперечные силы Qу. Эта сила представляет собой равнодействующую элементарных распределенных сил, лежащих в плоскости сечения. В этом случае в поперечных сечениях возникают не только нормальные, но и касательные напряжения.
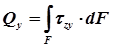
Возникновение касательных напряжений τ сопровождается появлением угловых деформаций. Поэтому, кроме основных смещений, свойственных чистому изгибу, каждая элементарная площадка сечения dF получает еще некоторые дополнительные угловые смещения, обусловленные сдвигом (рис. 10.16).

Рис. 10.16 Искривление поперечных сечений
Касательные напряжения распределены по сечению неравномерно, поэтому неравномерно будут распределены и угловые смещения. Это значит, что при поперечном изгибе в отличие от чистого изгиба поперечные сечения не остаются плоскими.
Найдем закон изменения касательных напряжений tzy=t при поперечном изгибе.
Для этого сначала рассмотрим случаи поперечного изгиба
(рис. 10.17):

Рис. 10.17 Эпюры Q и M при поперечном изгибе
Вычислить касательные напряжения проще всего через парные им напряжения, возникающие в продольных сечениях стержня. Выделим из бруска элемент длиной dz (рис. 10.18).
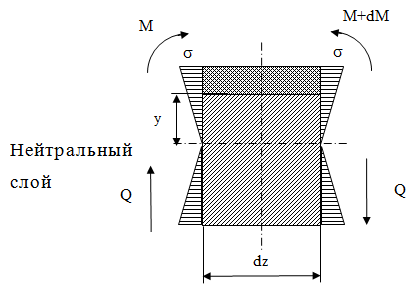
Рис. 10.18 Распределение касательных напряжений элемента бруска
При поперечном изгибе моменты, возникающие в левом и правом сечениях элемента, не одинаковы и отличаются на dM. Продольным горизонтальным сечением, проведенным на расстоянии у от нейтрального слоя, разделим элемент на две части и рассмотрим условия равновесия верхней части. Равнодействующая нормальных сил 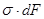 в левом сечении в пределах заштрихованной площади (отсеченной части) равна
в левом сечении в пределах заштрихованной площади (отсеченной части) равна
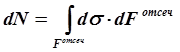
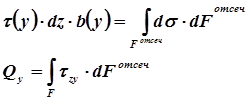
Полагая, что справедливо распределение в виде:
 , получим
, получим


 ,
,
где через у обозначена текущая ордината площадки dF. Разность нормальных сил в правом и левом сечении должна уравновешиваться касательными силами, возникающими в продольном сечении элемента (рис. 10.19)

Рис. 10.19 Распределение касательных напряжений τ(у) на участке dz
Полученный интеграл представляет собой статистический момент относительно оси х части площади, расположенной выше продольного сечения. Обозначим этот статистический момент через  , тогда
, тогда

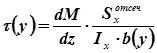
Учитывая, что 

Полученная формула носит название формулы Журавского. Она позволяет вычислить касательные напряжения, возникающие в продольных сечениях стержня.
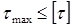
Полный расчет балки на прочность при поперечном изгибе:

и  ,
,
где Iх – осевой момент инерции сечения относительно центральной оси х;
b(y) – ширина живого сечения на уровне у;
Sхотсеч – статический момент площади, отсеченной уровнем у.
Пример
Найти закон изменения касательного напряжения t(у) на уровне у (рис. 10.20).
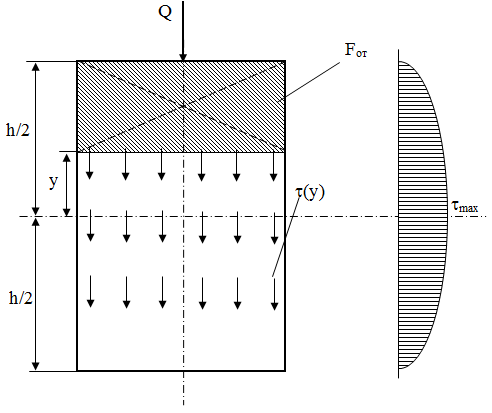
Рис. 10.20 Расчетная схема

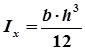
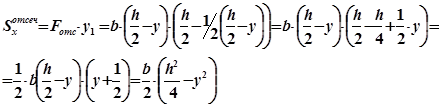
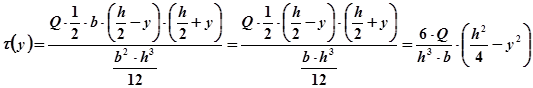
Закон изменения t представляет собой параболу.